ICOOL Reference Manual
R.C. Fernow et al
Brookhaven National Laboratory
.
Caveat Emptor
ICOOL is under active development at the present time. It is being made available as a potential
aid to members of the Neutrino Factory and Muon Collider Collaboration for studying ionization
cooling problems. Although considerable effort has gone into making the code give accurate
answers, it is ultimately the user’s responsibility to check that the program gives reasonable
answers to any specific problem.
Acknowledgments
I would like to thank my colleagues here at Brookhaven National Laboratory and in the Neutrino Factory and Muon Collider Collaboration for pointing out errors, making useful suggestions for improvements, and contributing new software to ICOOL.
Contents
1. Introduction
1.1 Comments in the ICOOL simulation control file for001.dat
1.2 Name substitution in the control file for001.dat
1.5 Keyboard input during execution
2.1 Problem title
2.4 Physics interactions control variables
2.5 Histogram definition variables
2.6 Scatterplot definition variables
2.7 Z-history definition variables
2.8 R-history definition variables
2.9 Emittance plane definition variables
2.10 Covariance plane definition variables
3. Region definition variables
SECTION start
of problem description
BEGS begin
repeating part of section
REPEAT start
of repeated
CELL start
of cell
SREGION start
of region
ENDREPEAT end of
repeating
ENDCELL end
of cell
ENDSECTION end
of problem description
APERTURE transverse
cut
BACKGROUND start
of background field definition
BFIELD defines background field
CUTV cut on ICOOL variable
DENP set
variable density profile
DENS adjust
material density
DISP randomly
displaces coordinates
DUMMY place
holder (do nothing) command
DVAR change
particle variable
EDGE fringe
field and other kicks for hard-edge fields
ENDB end
of background field definition
GRID define magnetic field
grid
OUTPUT writes
data to for009.dat
REFP RF
reference particle parameters
REF2 2nd
RF reference particle
RESET force
particle time to reference time
RKICK random
field kick
ROTATE rotates coordinates around specified axis
TAPER use
solenoid lattice with tapered currents
TILT randomly
rotates coordinates in 3D
TRANSPORT transforms
beam coordinates by matrix
! comment line
& name
substitution
3.3 Regular and pseudoregion command parameters
4. Field, material and geometry parameters
NONE no field
ACCEL accelerator
BLOCK thick solenoidal current block
BROD bent axial current rod
BSOL “bent solenoid” – combined solenoid and transverse fields
COIL coil
DIP vertical field sector dipole
EFLD electric field
FOFO alternating solenoid lattice
HDIP horizontal field sector dipole
HELIX
he
HORN magnetic horn
KICK kickers, deflection cavity
QUAD quadrupole
ROD current carrying rod
SEX sextupole
SHEET current sheet
SOL solenoid
SQUA skew quadrupole
STUS static user magnetic field
WIG wiggler
4.2 Material tags
VAC vacuum
GH gaseous hydrogen
GHE gaseous helium
LH liquid hydrogen
LHE liquid helium
LI lithium
BE beryllium
B boron
C carbon
TI titanium
FE iron
CU copper
W tungsten
HG mercury
PB lead
LIH lithium hydride
CH2 polyethylene
4.3 Geometry tags and parameters
NONE no material
ASPW azimuthally symmetric polynomial wedge
ASRW azimuthally symmetric radial wedge
CBLOCK cy
HWIN hemispherical absorber end
NIA non-isosceles absorber
PWEDGE asymmetric polynomial edge wedge
RING annular block
WEDGE
asymmetric
5. Other files
5.1 Input files
5.1.1 Beam input data
5.1.2 r-z grid magnetic field input data
5.1.3 RF cavity parameters
5.2 Output files
5.2.1 Program log file
5.2.2 Beam information at specified region
5.2.3 Postprocessor data file
5.2.4 Field
values on cy
5.2.5 Field values on 3D grid
5.2.6 RF diagnostics
5.2.7 Neutrino production data
5.2.8 Beam moments
5.2.9 Region summary table
ICOOL is a 3-dimensional tracking program that was originally written to study ionization
cooling of muon beams[1] . The program simulates particle -by- particle propagation through
materials and electromagnetic fields. Particles are tracked and regions are described using
"accelerator" coordinates. The program was written with low energy (1 MeV/c -- 1 GeV/c)
muons in mind, but tracking of electrons, pions, kaons, and protons is also possible.
The physics processes included are decays, delta rays, multiple scattering, energy loss and
straggling. Large sections of the physics interaction code was taken from GEANT v3.21 with
minimal interface changes.
Information is input to the code via an ASCII data file, described in section 2.
The incident beam particles can be generated from uniform or Gaussian distributions or read from an input file. The code can read its own output, so simulations can be staged. The particles are tracked through a sequence of regions that have a fixed length in z. In general a region is
cylindrical in shape and may be subdivided radially. Every region has a specified material and
field type associated with it. Groups of regions can be
can be superimposed over the region fields when tracking is done. In general the program takes
user-defined steps along the reference trajectory. For each step it updates the particle position and momentum, taking into account the local field, and corrects the particle's momentum for energy loss and multiple scattering in the step. There is an option for letting the program make adaptive step sizes.
ICOOL uses analytic and other procedures to compute field strengths at a given location. There are in general several model levels for each field type that gives the approximation used to calculate the field.
The program always generates an output log file. In addition, depending on control variable
settings, it may generate several other output files.
The quantities to plot come from a list of predefined quantities. Plots can be made at the
origin and after each region. Z-histories are plots made at user-defined steps in z. There are
options to save information about each particle after every region (or step) in an "n-tuple" file.
This manual defines all the parameters used by ICOOL. For an introduction to using ICOOL see the User’s Guide, ICguide.pdf
1.1 Comments
in the ICOOL simulation control file for001.dat
“Comments and blank lines can help format a control file so that it is more understandable to
human readers. The computer subroutines that read and parse control files don't want to see the
comments and blank lines. A new subroutine in ICOOL removes comments and blank lines
before the command processor parses them.
Rules for commenting a control file
A comment is any string of printable characters whose leftmost character is an exclamation
point.
! This is a comment.
!So is this.
! Additional exclamation points !! in a comment don't matter.
A whitespace is either a space or a horizontal tab.
A blank line either has no characters (except for the end-of-line terminator) or no characters
except whitespaces. Blank lines may be placed anywhere in the control file. They are ignored by
the command parser.
A comment line contains a comment, preceded by zero or more whitespaces. Comment lines
may be placed anywhere in the control file. They are ignored by the command parser.
An end-of-line comment is a comment placed to the right of a normal input line. End-of-line
comments may be placed at the end of any input line, separated from the data ICOOL is to parse
by zero or more whitespaces.
1.2342.345 !This is an end-of-line comment.
3.4564.567!So is this (valid but hard to read).
RING!This is valid even though "RING" will be read into a 6-character field.
RING !This is a more readable end-of-line comment.
The Use of Informal Comments
Though it is not forbidden, users are strongly discouraged from using "informal comments" --
those without leading exclamation points that are imagined to be out of view of the parser. There
are numerous ways to go wrong. For example, free format reads can extract data from more than
one input line; an informal comment on the end of any but the last line will generally produce an
error. An informal comment following a text string must come with enough preceding spaces to
fill the input field with spaces. All of these potential problems are avoided by using formal
comments with leading exclamation points.” {S.B.}
Any parameter in the input command file for001.dat can be defined symbolically using the command
&SUB name value
Following this command any occurrence of the text string
&name
is replaced with its value. Do not use
A variant allows
sca
&SCL NameString type value
NameString is a set of characters. All previously defined names that begin with this character string will be scaled. The variables may be either additively or multiplicatively scaled, depending on the value of type = {*, +}. The amount of scaling is determined by value.
Drift space example with a
scatterplot of x vs. y
&cont npart=500 / ! control variables
&bmt /
! beam definition
1 2 1. 1
! Gaussian definition of muon beam
0. 0. 0. 0. 0. 0.200 ! means
3e-3 3e-3 0.01 0.005 0.005 0.010 ! sigmas
0
! no imposed beam correlations
&ints /
! use default interactions
&nhs /
! no histograms
&nsc nscat =1 /
! define 1 scatter plot
-0.10 5e-3 40 1 2 -0.10 10e-3 20 2 2
&nzh /
! no z-histories
&nrh /
! no r-histories
&nem /
! no 2-D emittance calculations
&ncv /
! no covariance calculations
SECTION
! start problem definition
SREGION
! define a region
1.00 1 0.003 ! length, 1 radial subregion, step
1 0. 0.10 ! radial extent
NONE
! no associated field
0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
VAC ! vacuum material
CBLOCK
! cylindrical block geometry
0. 0. 0. 0. 0. 0. 0. 0. 0.
0.
ENDSECTION
! end of problem definition
More complicated example
with REFP, GRID, and CELL commands
&cont npart=500 / ! control variables
&bmt /
! beam definition
1 2 1. 1
! Gaussian definition of muon beam
0. 0. 0. 0. 0. 0.200 ! means
3e-3 3e-3 0.01 0.005 0.005 0.010 ! sigmas
0
! no imposed beam correlations
&ints /
! use default interactions
&nhs /
! no histograms
&nsc /
! no scatter plots
&nzh /
! no z-histories
&nrh /
! no r-histories
&nem /
! no 2-D emittance calculations
&ncv /
! no covariance calculations
SECTION
! start problem definition
REFP
! define a reference particle
2 0.186 0. 0. 3
GRID
! save field from file of current
1
! sheets in grid array #1
SHEET
! use current sheets
0 20 0.01 0.01 1.51
0.11 15. 0 21 0 0 0 0 0 0
CELL
! begin cell structure
16
! repeat 16 times
.true.
! alternate field polarity
SHEET
! define the associated cell field
5 1 2 0 0 0
0 0 0 0 0 0 0 0 0
SREGION
! define the region inside the cell
1.50 1 0.003 ! length, 1 radial subregion, step
1 0. 0.10 ! radial extent
ACCEL
! rf cavity field
2 805 36 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0.
VAC ! vacuum material
CBLOCK
! cylindrical block geometry
0. 0. 0. 0. 0. 0. 0. 0. 0.
0.
ENDCELL ! end this cell structure
ENDSECTION
! end of problem definition
1.5 Keyboard input during execution
ICOOL recognizes two keyboard inputs while it is executing.
p pauses execution until the Enter key is pressed
x stops execution with the current particle and region and executes any end of run diagnostics.
The input file consists of:
1. problem title
2. general control variables
3. beam generation variables
4. physics interactions control variables
5. histogram definition variables
6. scatterplot definition variables
7. Z-history definition variables
8. R-history definition variables
9. emittance plane definition variables
10. covariance plane definition variables
11. region definition variables
The first 10 types of these variables are discussed in this section. Region definition variables are discussed in section 3.
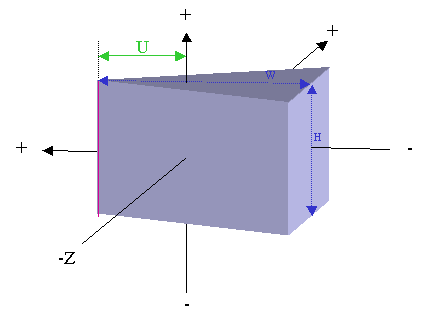
A 79 character title for the problem. This title is written onto files 2, 4, and 9, described
below.
Namelist: CONT
BETAPERP (R) beta value to use in calculating amplitude variable A2
BGEN (L) if .true. => generate initial beam particles, otherwise read input from
FOR003.DAT (true)
BUNCHCUT (R) maximum time difference allowed between a particle and the reference
particle [s] (1E6)
BZFLDPRD (R) Bz for solenoid at location of production plane (0.) This is used for output to file for009.dat and for canonical angular momentum correction.
DECTRK (L) if .true. => continue tracking daughter particle following decay (false)
DIAGREF (L) if .true. => specify pZ and t relative to the reference particle for ICOOL internal diagnostics (F)
EPSF (R) desired tolerance on fractional field variation, energy loss, and
multiple scattering per step (0.05)
EPSREQ (R) required tolerance on error in tracking parameters (1E-3) This parameter is only used if varstep = true
EPSSTEP (R) desired tolerance in spatial stepping to reach each destination plane
[m] (1E-6)
FFCR (L) if .true. => inserts form feed and carriage returns in the output log file
so there are two plots per page starting at the top of a page (false)
FORCERP (L) if .true. => set x, y, Px, and Py for reference particle to 0 for each
new REFP command and for each ACCEL region with phasemodel=4. (true)
FSAV (L) if .true. => store particle info at plane IZFILE into file
FOR004.DAT. (false)It is possible to get the initial distribution of particles that get a given
error flag be setting the "plane"=IFAIL #. It is possible to get the initial distribution of particles
that successfully make it to the end of the simulation by setting the plane= -1.
FSAVSET (L) if .true. => modify data stored using FSAV in FOR004.DAT to have
z=0 and times relative to reference particle at plane IZFILE. (false)
F9DP (I) number of digits after the decimal point for floating point variables in FOR009.DAT {4,6,8,10,12,14,16,17} (4) F9DP=17 gives 16 digits after the decimal point and 3 digits in the exponent.
GOODTRACK (L) if .true. and BGEN=.false. => only accepts input data from
file FOR003.DAT if IPFLG=0.; if .false. => resets IPFLG of bad input tracks to 0 (this allows
processing a file of bad tracks for diagnostic purposes) (true)
IZFILE (I) z-plane where particle info is desired when using FSAV. Use 1 to
store beam at production. Saves initial particle properties for bad tracks if IZFILE=IFAIL #.
Saves initial particle properties for tracks that get to the
end of the simulation if IZFILE=-1.
IZFILE should point to the end of a REGION or to an APERTURE , ROTATE or
TRANSPORT
pseudoregion command.
MAGCONF (I) if 19 < MAGCONF=mn < 100 => reads in file FOR0mn.DAT, which
contains data on solenoidal magnets. Used with SHEET, model 4.(0)
MAPDEF (I) if 19 < MAPDEF=mn < 100 => reads in file FOR0mn.DAT, which
contains data on how to set up field grid. Used with SHEET, model 4.(0)
NEIGHBOR (L) if .true. => include fields from previous and following regions when
calculating field. (false) This parameter can be used with soft-edge fields when the magnitude of
the field doesn't fall to 0 at the region boundary. A maximum of 100 regions can be used with this feature.
NEUTRINO (I) if 19 < NEUTRINO=mn < 100 => writes out file FOR0mn.DAT,
which contains neutrino production data. See section 5.2 for the format. (0)
NNUDK (I) # of neutrinos to produce at each muon, pion and kaon decay. (1)
NPART (I) # of particles in simulation. The first 300,000 particles are stored in memory. Larger numbers are allowed in principle since ICOOL writes the excess particle information to disc. However, there can be a large space and speed penalty in doing so.
NPRNT (I) # of diagnostic events to print out to log file (-1)
NSECTIONS (I) # of times to repeat basic cooling section (1)
This parameter can be used to repeat all the commands between the SECTION and ENDSECTION commands in the problem definition. If a REFP command immediately follows
the SECTION command, it is not repeated.
NTUPLE (L) if .true. => store information about each particle after every
region in file FOR009.DAT. This variable is forced to be false if RTUPLE= true.(false)
NUTHMIN (R) Minimum polar angle to write neutrino production data to file.
[radians] (0.)
NUTHMAX (R) Maximum polar angle to write neutrino production data to file.
[radians] (3.14)
OUTPUT1 (L) if .true. => write particle information at production (plane 1) to the
postprocessor output file for009.dat. (false)
PHANTOM (L) if .true. => force particle to keep initial transverse coordinates after
every step. This is useful for making magnetic field maps. (false)
PHASEMODEL (I) controls how the phase is determined in rf cavities. (1)
1: takes phase directly from ACCEL command [degrees]
2 - 6: takes phase model from REFP command
7: reads phases in from file FOR0mn.DAT, where RFPHASE=mn. See sec. 5.1.
PRLEVEL (I) controls level of print information to log file (for NPRINT
events);higher # gives more print(1)
1: values at end of region
2: + values at end of each time step
3: + E,B values at each step
4: + information in cylindrical coordinates
PRNMAX (I) Sets maximum number of steps to generate print out inside a region
(300)
PZMINTRK (R) Sets the value of Pz below which tracking stops. [GeV/c] (0.001)
RFDIAG (I) if 19 < RFDIAG=mn < 100 => writes rf diagnostic information at the
end of each accelerator region to file FOR0mn.DAT. (0)
RFPHASE (I) if PHASEMODEL=5 => reads rf phases, frequencies and gradients
for the cavities from file FOR0mn.DAT, where RFPHASE=mn
and 19 < mn < 100 (0)
RNSEED (I) random number seed (-1) Set to a negative integer.
RTUPLE (L) if .true. => particle information in file FOR009.DAT is generated after
every RTUPLEN steps. (false)
RTUPLEN (I) # of steps to skip between RTUPLE generated outputs. (5)
RUN_ENV (L) if true => run ICOOL in beam envelope mode, i.e. no tracking (false)
For solenoidal channels only.
SCALESTEP (R) factor that modifies all step sizes in a problem simultaneously (1.0)
Only works in fixed stepsize mode.
SPIN (L) if .true. => include calculation of polarization. (false)
SPINMATTER (I) controls whether muon depolarization effects in matter are simulated
(0)
0: no depolarization simulation
1: depolarization simulation using Rossmanith model
2: depolarization simulation using spin flip probabilities
SPINTRK (I) controls whether spin variables are tracked (0)
0: no spin tracking
1: track spin in muon rest frame using BMT equations
STEPMAX (R) maximum step size that can be used for variable stepping [m]
(1)
STEPMIN (R) minimum step size that can be used for variable stepping [m]
(1E-5)
STEPRK (L) if .true. => use 4th order Runge-Kutta integrator for tracking.
Otherwise it uses the Boris push method in straight regions. (true)
SUMMARY (L) if true => writes region summary table to for007.dat (true)
TERMOUT (L) if .true. => write output to terminal screen (true)
TIMELIM (R) time limit for simulation [min] (1E9)
VARSTEP (L) if .true. => use adaptive step size; otherwise use fixed step ZSTEP
(until reaching the last step in a region). This variable is forced to be false (1) in wedge material
regions, (2) when the number of radial regions is greater than 1, and (3) when PHASEMODEL=2. (true)
2.3 Beam generation variables
Namelist: BMT
NBEAMTYP (I) # of beam types, e.g. particles of different mass {1-5} (1)
BMALT (L) if true => flip sign of alternate particles when BGEN = true. (false)
Other input variables
The following input is only read if BGEN = .true.
(2-4 repeated for each beam type)
2.1) PARTNUM (I) particle number
2.2) BMTYPE (I) beam type { magnitude = 1:e 2:mu 3:pi 4:K 5:p; sign = charge}
2.3) FRACBT (R) fraction of beam of this type {0-1} The sum of all fracbt(i) should =
1.0
2.4) BDISTYP (I)beam distribution type {1:Gaussian 2:uniform circular segment}
If BDISTYP = 1
3.1) X1BT(i),i=1,3 (R) mean value of x,y,z for this beam type [m]
3.2) P1BT(i),i=1,3 (R)mean value of px,py,pz for this beam type [GeV/c]
4.1) X2BT(i),i=1,3 (R)standard deviation of x,y,z for this beam type; assumes Gaussian [m]
4.2) P2BT(i),i=1,3 (R)standard deviation of px,py,pz for this beam type;
assumes Gaussian [GeV/c]
If BGEN=false, VARSTEP=false, and a particle in the input file has a starting z location z0 greater than 0, then the particle will not be tracked until the z stepping logic in the code reaches z0.
If BDISTYP = 2
3.1) X1BT(1),X2BT(1) (R)r_low,r_high [m] {>0}
3.2) X1BT(2),X2BT(2) (R) phi_low,phi_high [degrees]
3.3) X1BT(3),X2BT(3) (R) z_low,z_high [m]
4.1) P1BT(1),P2BT(1) (R) Pr_low,Pr_high [GeV/c] {>0}
4.2) P1BT(2),P2BT(2) (R) Pphi_low,Pphi_high GeV/c]
4.3) P1BT(3),P2BT(3) (R) Pz_low,Pz_high [GeV/c]
5) NBCORR (I) # of beam correlations {0-10}
(6-repeated NBCORR times)
6.1) CORRTYP (I) correlation type
6.2) CORR1(i) (R) correlation parameter 1
6.3) CORR2(i) (R) correlation parameter 2
6.4) CORR3(i) (R) correlation parameter 3
CORRTYP = 1 angular momentum appropriate for constant solenoid field
= 2 Palmer amplitude correlation
= 3 rf bucket, small amplitude ellipse
= 4 rf bucket, small amplitude separatrix
= 5 rf bucket, large amplitude separatrix
= 6 Twiss parameters in x Px
= 7 Twiss parameters in y Py
= 8 (not used)
= 9 equal time in solenoid
=10 Balbekov version of amplitude-energy
=11 dispersion
For CORRTYP = 1
2 solenoid field [T]
Value should equal effective solenoid field in the body of the magnet.
For CORRTYP = 2
2 correlation strength
3 effective β^ [m]
dPz = CORR1 * ( (r/CORR2)^2+X'^2 + Y'^2)
For CORRTYP = 3,4
2 peak electric field on axis[MV/m]
3 synchronous phase [degrees]
4 rf frequency [MHz]
Set desired σZ in input beam definition. Set σPz = 0.
For CORRTYP = 5
2 peak electric field on axis[MV/m]
3 synchronous phase [degrees]
4 rf frequency [MHz]
Set σZ and σPz = 0 in input beam definition.
For CORRTYP = 6
2 Twiss alpha parameter
3 Twiss beta parameter [m]
4 Twiss epsilon parameter[m]
The spread in x and Px in the beam definition are ignored. For Gaussian distributions epsilon is
the rms geometrical emittance. For uniform distributions it specifies the limiting ellipse.
For CORRTYP = 7
2 Twiss alpha parameter
3 Twiss beta parameter [m]
4 Twiss epsilon parameter[m]
The spread in y and Py in the beam definition are ignored. For Gaussian distributions epsilon is
the rms geometrical emittance. For uniform distributions it specifies the limiting ellipse.
For CORRTYP = 9
2 desired axial beta (=v/c) value βo
3 azimuthal angle of transverse momentum [deg]
Set up with pz and σPz such that βz > βo. Set up initial pt = 0. This correlation determines the pt
for a given pz that gives all the initial particles the same βo. If parameter 3 is 0, the azimuthal
angle is chosen randomly.
For CORRTYP = 10
2 Eref [GeV]
3 Babs [ T ]
4 σE [GeV]
AB2 = (pT/mc)2 + (e Babs r / 2 mc2)2
E = Eref { 1 + AB2 }0.5 + σE
dE: random energy deviation taken from GAUS(0, σE)
Enter the normal beam input σPz = 0.
For CORRTYP = 11
2 value [m or rad]
3 pREF [GeV/c]
4 type flag
1: x
2: y
3: x’
4: y’
2.4 Physics interactions control variables
LDEDX (L) if .true. => simulate mean ionization energy loss dE/dx (true)
LSCATTER (L) if .true. => simulate multiple scattering (true)
LSTRAG (L) if .true. =>
simulate energy stragg
LDECAY (L) if .true. => simulate particle decays (true)
LDRAY (L) if .true. => simulate discrete energy loss from delta rays (true)
When LDRAY is true, the program forces the parameters DELEV=3 and STRAGLEV=5.
LINTERACT (L) if .true. => simulate inelastic nuclear interactions of pions, kaons and protons (false)
LSPACE (L) if .true. => consider effects of space charge (false)
LELMS (L) if .true. => use ELMS model[2] for energy loss and scattering (false).
When this command is true an external file ELMSCOM.TXT must
be provided. This file consists of two
\muon\elmsdb\rundirectory.txt
\muon\elmsdb\elmsfv3run
ELMS only works in regions containing hydrogen (the SCATLEV model is used in other regions). For hydrogen regions use a stepsize around 5 mm for maximum accuracy. A stepsize of 1 mm gives significantly worse results.
LSAMCS (L)
if .true. => use SAMCS model[3]
of correlated stragg
DELEV (I) model level for dEdx (2)
1: Bethe-Bloch
2: Bethe-Bloch with density effect
3: restricted Bethe-Bloch with density effect
4: test mode with dE = const * dz, independent of velocity and angle
SCATLEV (I) model level for multiple scattering (6)
1: Gaussian( 0, Rossi-Greisen )
2: Gaussian( 0,
3: Gaussian( 0, Lynch-Dahl )
4: Bethe version of Mo
5:
6: Fano (with
7: Tollestrup (with
Level 2 contains a logarithm term in computing the Gaussian width, so it is not useful for general monte carlo work. It gives an accurate estimate of the width of the distribution when the step size is the same as the region size. In models 4, 6, and 7 when the effective number of scatters is less than 20 Rutherford scattering is used with the actual number of scatters in a given step taken from a Poisson distribution.
STRAGLEV (I) model level for stragg
1: Gaussian( Bohr )
2: Landau distribution
3: alternate routine for Landau distribution
4: Vavilov distribution (with
appropriate Landau and Gaussian
program)
5: restricted energy fluctuations from continuous processes with energy below DCUTx.
DECLEV (I) model level for particle decays (1)
1: uniform polar decay angle for daughter particle in parent rest frame
2: 90 degree polar decay angle for daughter particle in parent rest frame
3: uniform polar decay angle for daughter particle in parent rest frame; no mu-->e decays.
4: 90 degree polar decay angle for daughter particle in parent rest frame; no mu->e decays
5: uniform polar decay angle for daughter particle in parent rest frame; no mu-->e decays;
save accumulated fractional decay length in POL(1).
INTLEV (I) model level for nuclear interactions (1)
1: stop tracking after an interaction
2: stop tracking after an interaction, except for protons which generate a pion from the Wang distribution.
SPACELEV (I) model level for space charge (3)
1: image charge of moving bunch in
cy
2: crude transverse space charge
for free space app
3: Gaussian bunch space charge
(transverse and longitudinal) for free space app
regions
4: same as model 3 for single bunch in a bunch train. All the particles are superimposed
on 1 bunch given by parameter FRFBUNSC. Adjust PARBUNSC accordingly.
DCUTE (R) kinetic energy of electrons, above which delta rays are discretely
simulated[GeV] (1E-1)
DCUTM (R) kinetic energy of muons and other heavy particles, above which delta
rays are discretely simulated [GeV] (1E-1)
ELMSCOR (I) 0: run ELMS without correlations (0)
1: run ELMS with correlations
FACFMS (R) factor to correct the Z(Z+1) term in the characteristic angle squared
χC2
in Mo
FACMMS (R) factor to correct screening angle squared χA2 in Moliere multiple
scattering theory (1.0)
FASTDECAY (L) if true => use unphysical decay constants to make {μ,π,K} decay
immediately. (false)
FRFBUNSC (R) RF frequency used for space charge model 4. [MHz] (201.)
PARBUNSC (R) number of muons per bunch for space charge calculation (4E12)
PDELEV4 (R) momentum for DELEV=4 calculation (0.200)
WANGA (R) Wang parameter A (90.1) The Wang distribution is given by
d2s/dp dW = A pMAX x (1-x) exp{-BxC – DpT} where x = pL / pMAX .
WANGB (R) Wang parameter B (3.35)
WANGC (R) Wang parameter C (1.22)
WANGD (R) Wang parameter D (4.66)
WANGPMX (R) Wang parameter pMAX (1.500) The sign of this quantity is used to select π+ or π- production.
WANGFMX (R) The maximum value of the Wang differential cross section (13.706)
2.5 Histogram definition variables
NHIST (I) # of histograms{0-20} (0)
HAUTO (L) if .true.=>histograms are scaled for no overflows (true)
HCPRN (I) if 19 < HCPRN < 100 => histogram contents are written to file FOR0nm.DAT
Other input variables
(2-repeated for each histogram)
2.1) HXMIN (R) minimum value
2.2) HDX (R) step size
2.3) NHBINS (I) total # of bins {1-50}
2.4) IHVAR (I) a flag indicating variable to histogram
2: Y 12: Y'
3: Z 13: (space angle)
4: Px 14: r 24: 34: Ex
5: Py 15: phi 25: 35: Ey
6: Pz [2] 16: Pr 26: 36: Ez
7: ct[2] 17: Pphi 27: 37: Sx
8: Pmag 18: Lz 28: A^2 [1] 38: Sy
9: E 19: L^2 29: r^2 39: Sz
10: KE 20: (arclength) 30: muon helicity 40:(phase)
2.5) IHDES (I) the s-plane location for the histogram
Note that s-regions are not the same as physical regions, since they also count any pseudoregions, such as OUTPUT or ROTATE, that may be present. You can find the s-region listed in the left most column of the region summary table (FOR007.DAT).
1: variables at production
s: variables at s-region s
-1: variables at production that make it to the end of the simulation
(only IHVAR=1..7 are defined )
ifail : variables at production for events when this ifail occurs {< -10}
(only IHVAR=1..7 are defined )
[1] To plot A2, use the BETAPERP control variable.
[2] If DIAGREF is true, the difference with respect to the reference particle is used.
2.6 Scatterplot definition variables
NSCAT (I) # of scatterplots {0-20} (0)
SAUTO (L) if .true. => scatterplots are scaled for no overflows (true)
Other input variables
(2-repeated for each scatterplot)
2.1) SXMIN (R) minimum x value
2.2) SDX (R) step size in x
2.3) NSXBIN (I) total # of x bins {1-50}
2.4) ISXVAR (I) a flag indicating x variable to scatterplot
(see definitions in IHVAR above)
2.5) ISXDES (I) the s-plane location for the x variable in the scatterplot (see below)
2.6) SYMIN (R) minimum y value
2.7) SDY (R) step size in y
2.8) NSYBIN (I) total # of y bins {1-23}
2.9) ISYVAR (I) a flag indicating y variable to scatterplot
(see variable definitions in IHVAR above)
2.10) ISYDES (I) the s-plane location for the y variable in the scatterplot
Note that s-planes are not the same as physical regions, since they also count any pseudoregions,
such as OUTPUT or ROTATE, that may be present. You can find the s-region listed in the left
most column of the region summary table (FOR007.DAT).
1: variables at production
s: variables at s-plane s
-1: variables at production that make it to the end of the simulation
(only IHVAR=1..7 are defined at production)
ifail: make scatterplot of events when ifail occurs. Both ISXDES and
ISYDES must equal ifail.
2.7 Z-history definition variables
NZHIST (I) # of Z-histories {0 - 20} (0)
ZHAUTO (L) if .true. => z-histories data is scaled to fill plot (true)
ZHPRIN (L) if .true. => values printed in log file (false)
Other input variables
(2-repeated for each z-history)
2.1) NZHPAR (I) # of particles to plot {1-10}
2.2) ZHXMIN (R) minimum value of z to plot [m]
2.3) ZHDX (R) z distance between plot values [m]
2.4) NZHXBIN (I) #of z points {1-70}
2.5) ZHYMIN (R) minimum value of variable to plot
2.6) ZHYMAX (R) maximum value of variable to plot
2.7) IZHYVAR (I) variable flag (see definitions in IHVAR above)
2.8 R-history definition variables
Computes minimum, maximum, mean and standard deviation of the distribution of all particles
for a variable at the end of regions
NRHIST (I) # of R-histories {0 - 10} (0)
RHAUTO (L) if .true. => R-histories data is scaled to fill plot (true)
RHPRIN (L) if .true. => values printed in log file (false)
Other input variables
(2-repeated for each R-history)
2.1) IRHZMIN (I) starting region number
2.2) IRHDZ (I) increment in region number along horizontal axis
2.3) RHYMIN (R) minimum value of variable to plot
2.4) RHYMAX (R) maximum value of variable to plot
2.5) IRHYVAR (I) variable flag (see definitions in IHVAR above)
2.9 Emittance plane definition variables
Calculates 2-D emittances at specified planes
NEMIT (I) # of s-planes where the emittance or polarization should be
calculated {0-100}(0)
DISCORR (L) if .true. => correct x and y emittance calculations for dispersion (false)
PXYCORR (L) if .true. => Px and Py are corrected (for the emittance calculation) for
the vector potential in a solenoid field.(false)
IPZCOR (I) flag for correcting the normalized longitudinal emittance for the
Pz versus transverse amplitude correlation. (0)
0: no correction
1: correct using Palmer amplitude, AP
AP2 = x’2 + y’2 +(x/βT)2 + (y/ βT)2
2: correct using Balbekov transverse amplitude,
AB
AB2
= (pT/mc)2 + (eBr/2mc)2
SIGMACUT (L) if .true. => tails of {x ... Pz} are cut at SIG_CUT sigmas before the
emittance is calculated. (true)
SIG_CUT (R) # of sigmas to cut off tails of {x ... Pz} for the emittance calculation.
(4.)
Other input variables
(repeated for each emittance plane)
2) IEMDES(i),i=1,N (I) s-plane identification # where emittance or POLARIZATION is
calculated. Note that s-planes are not the same as physical regions, since they also
count any pseudoregions, such as OUTPUT or ROTATE, that may be present. You can find the
s-region listed in the left most column of the region summary table in the log output file
(FOR002.DAT).
1: variables at production
s: variables at s-plane s
Output data is normalized relative to first plane in IEMDES list. Note that in a solenoidal field
emittances are only correctly computed when PXYCORR=true or at s-planes where B = 0. For emittances at the production plane use the control variable BZFLDPRD. A returned emittance value of -998 or -999 indicates the program could not calculate a sensible emittance.
2.10 Covariance plane definition variables
Calculates covariance matrices and related “LBNL” emittances
NCOVAR (I) # of s-planes where the covariance should be calculated {0-100} (0)
Other input variables
2) ICVDES(i),i=1,N (I) s-plane identification # where covariance is
calculated. Note that s-planes are not the same as physical regions, since they also
count any pseudoregions, such as OUTPUT or ROTATE, that may be present. You can find the
s-region listed in the left most column of the region summary table in the log output file
(FOR002.DAT).
1: variables at production
s: variables at s-plane s
Region commands (A4) Use UPPER case.
Start of cooling section region definition; the data must end with an ENDSECTION ; it can
enclose any number of other commands. If it is desired to repeat the section definitions, the
control variable NSECTIONS should be set >1 and a BEGS command is used to define where to
start repeating.
This marks the beginning of the part of region definitions that will be repeated with the NSECTIONS control variable. This command doesn’t do anything if NSECTIONS = 1.
3) REPEAT
Start of a repeating
command. This can be used to repeat regions inside a cell. The repeat loop can enclose any
number of {SREGION, APERTURE, DENS, DISP, DUMMY, DVAR, EDGE, OUTPUT, REFP, REF2, RESET, RKICK, ROTATE, TILT, TRANSPORT} commands. Repeat sections cannot be nested in other repeat sections. (see parameters below)
4) CELL
Start of a repeating
command. The cell loop can enclose any number of commands listed above under REPEAT plus REPEAT and ENDREPEAT commands. It has an associated cell field, which is superimposed on the individual region fields. Cell sections cannot be nested in other cell sections. (see parameters below)
5) SREGION
Start of new s-region. Describes field and material properties. (see parameters below)
6) ENDREPEAT End of REPEAT data block.
7) ENDCELL End of CELL data block.
8) ENDSECTION
End of region data definition; the section of data is repeated NSECTIONS times.
These commands are read in (A4) format.
APERTURE Collimates beam at aperture (see parameters below)
CUTV Cut on ICOOL variable (see parameters below)
DENP Set variable density profile (see parameters below)
DENS Adjust material density (see parameters below)
DISP Randomly displaces particle coordinates (see parameters below)
Dummy placeholder in the problem definition. This can be used to save a place for an OUTPUT
command in the problem definition. This makes it more convenient to keep the size of the for009.dat file manageable. (no parameters)
DVAR Change parameter value for all particles (see parameters below)
EDGE Fringe field and other kicks for hard-edged field models (see parameters below)
GRID Defines new magnetic field grid (see parameters below)
Enables the writing of particle information at the end of the following region to FOR009.DAT.
This command will only function if both NTUPLE and RTUPLE are false. (no parameters).
REFP Define RF reference particle properties (see parameters below)
REF2 Define 2nd RF reference particle properties (see parameters below)
RESET Change time of all particles to reference particle time (no parameters)
RKICK Random magnetic kicks (see parameters below)
ROTATE Coordinate system rotation (see parameters below)
TAPER Solenoid lattice with tapered currents (see parameters below)
TILT Randomly rotates particle coordinates in 3D (see parameters below)
TRANSPORT
User input of transport matrix. A reference particle must be defined to use this command. (see
parameters below)
BACKGROUND
Start of a background field definition section. the data must end with an ENDB command. This
section may include any number of BFIELD commands. (see parameters below)
BFIELD Define background field (see parameters below)
ENDB End definition of background field (see parameters below)
! (see discussion on comments in the Introduction)
& (see discussion on name substitution in
the Introduction)
3.3 Regular and
pseudoregion command parameters
It is important that parameters listed like 1.1 to 1.4 below
appear on the same line in
the input file and that parameters like 2.1 start a new line.
1.1) IAPERTYPE (I) 1:elliptical, 2:rectangular, 3:normal quad, 4:skew quad
For IAPERTYPE = 1
1.2) APERLIM1 (R) x half-width [m]
1.3) APERLIM2 (R) y half-width [m]
1.4) 0. (R) parameter not used
For IAPERTYPE = 2
1.2) APERLIM1 (R) lower limit [m]
1.3) APERLIM2 (R) upper limit [m]
1.4) 1:x 2:y (R) direction
For IAPERTYPE = 3 or 4
1.2) RPOLE (R) distance from axis to pole piece [m]
1.3) ROUT (R) distance from axis to outer useful radius [m]
1.4) PARAB (R) distance from vertex to focus of parabola [m]
1.1) BENTBKG (L) set TRUE if reference trajectory is curved
1.2) PREFBKG (R) reference momentum thru background grid [GeV/c]
1.3) ZTOTALBKG (R) total incremental length in z to use this BG field [m]
2.1) XLOBKG (R) low x value of background grid [m]
2.2) DXBKG (R) bin size in x for background grid [m]
2.3) NXBKG (I) number of x bins {<31}
2.4-6) YLOBKG, DYBKG, NYBKG(similar to corresponding x parameters)
2.7) ZLOBKG (R) minimum distance into background region before using
background field, i.e. the
background field is 0 for distances
into background region less than ZLOBKG.
The maximum distance to use the background field is ZLOBKG+ZTOTALBKG.
Distances in z are in relative units, i.e. they start at 0.
2.8) DZBKG (R) bin size in z for background grid [m]
2.9) NZBKG (I) number of z bins{<201}
2.10) INTERBKG (I) interpolation order for background grid {1-3}
(Command parameters continued)
BFIELD
1.1) ZOFFBKG (R) offset in z before starting edge of this field contribution [m]
This can be used to start field contributions at varying distances from the beginning of the current
background field.
1.2) RMAXBKG (R) maximum radius at which this field should be applied to the
background grid [m]
1.3) ZMINBKG (R) Starting z location at which to consider this field contribution [m]
1.4) ZMAXBKG (R) Ending z location at which to consider this field contribution [m]
ZMINBKG and ZMAXBKG are measured from the start of the current background field. If
round-off error causes the last BG field point to be in error, increase ZMAXBKG by a small
amount, e.g. by 0.001.
..
2) BFTAG (A4) background field tag (see FTAG values below)
3) BFPARM (R) 15 parameters describing field (see specific field type below)
1) NCELLS (I) Number of times to repeat the commands in this cell block.
2) CELLFLIP (L) If .true. => flip cell field for alternate cells
3)CFTAG (A4) Field tag for field that is superimposed over all the regions
in this cell; see FTAG values below.
4) CFPARM (R) 15 parameters describing field (see specific field type below)
1.1) ICOOL variable index {1-12}
See variable
1.2) relational test
1: < (less than)
2: > (greater than)
1.3) value (R)
(Command parameters continued)
1.1) material (A4) material tag
1.2) direction (I) 1:x 2:y 3:r
1.3) coefficient a (R)
1.4) coefficient b (R)
1.5) coefficient c (R)
1.6) coefficient d (R)
Let v be the variable determined by the direction parameter. Then the density is a function of v given by
ρ = a + b v + c v2
+ d v3
This command can only affect the density of one material at a time. To
disable this function execute a DENP command with direction=-1.
DENS
1.1) material (A4) material tag
1.2) factor (R) factor to change current density value
1.1) D (R) σ of displacement distribution [m]
1.2) PHI (R) angle of rotation w.r.t. x axis in x-y plane [deg]
If PHI = -1 => angle of rotation axis is chosen randomly from a uniform distribution.
DVAR
1.1) variable
index (I) see variable
1.2) change (R) amount to change variable [m, GeV/c, s, GeV]
1.3) apply to (I) {0,1,2}
0: all particles
1: reference particle only
2: normal particles only
(Command parameters continued)
1) edge type (A4) {SOL, DIP, HDIP,DIP3,QUAD,SQUA,SEX, BSOL,FACE}
2.1) model # (I) {1}
2.2-5) p1, p2, p3,p4 (R) model-dependent parameters
Edge type = SOL
p1: BS [T]
If the main solenoid field is B, use p1=-B for the entrance edge and p1=+B for the exit edge.
Edge type = DIP
p1: BY [T]
Edge type = HDIP
p1: BX [T]
Edge type = DIP3
p1: rotation angle [deg]
p2: BY0 [T]
p3: flag 1:in 2:out
Edge type = QUAD
p1: gradient [T/m]
Edge type = SQUA
p1: gradient [T/m]
Edge type = SEX
p1: b2 [T/m2] (cf. C. Wang & L. Teng, MC 207)
Edge type = BSOL
p1: BS [T]
p2: BY [T]
p3: 0 for entrance face, 1 for exit face
Edge type = FACE
This gives vertical focusing from rotated pole faces.
p1: pole face angle [deg]
p2: radius of curvature of reference particle [m]
p3: if not 0 => correct kick by the factor 1 / (1+δ)
p4: if not 0 => apply horizontal focus with strength = (-vertical strength)
If a FACE command is used before and after a sector dipole ( DIP ), you can approximate a rectangular dipole field.
The DIP, HDIP, QUAD, SQUA, SEX and BSOL edge types use Scott Berg’s HRDEND routine to find the change in transverse position and transverse momentum due to the fringe field.
(Command parameters continued)
1) (I) file # of field output on the grid {20-99}. Set this <20 if you
don't want an output file. See output file section 5.2.
GRID
This can be used to define a 2D r-z grid, a 2D x-y grid, or a 3D x-y-s grid, depending on the value of the field type.
(1) r-z grid
1) grid number (I) {1-4}
2) field type (A4) { BLOCK , COIL , SHEET , SOL }
3) field parameters (R) (enter 0. for unused parameters)
3.2) file # of input COIL , SHEET , etc. data {20-99}
If the file number is entered as a negative number, the current densities in the external file are all reversed in polarity. The external file formats are described under the field models BLOCK(2), COIL(3), SHEET(3) and SOL(6).
3.3) dz for grid [m]
3.4) dr for grid [m]
3.5) total z length of grid [m] The maximum number of z grid points is 5000.
3.6) total r length of grid [m] The maximum number of r grid points is 100.
3.7) z cut parameter for ignoring current elements ( COIL and SHEET only)
3.9) file # for field output on the grid (or 0 for none) {20-99}
The format of the output file generated by parameter 9 is listed in section 5.2.
3.10) Longitudinal shift parameter. If a longitudinal grid index JZ is entered here, the field grid stored in memory starts at JZ, wraps through the beginning of the grid and ends at longitudinal index JZ-1.
3.11) Current element scaling factor. Set to 1.0 for no scaling.
3.12) Calculation algorithm for BLOCK only.
0: from numerical integration
1: from series
(Command parameters continued)
(2) x-y grid
1) grid number (I) {1-4}
2) field type (A4) { BROD }
3) field parameters (R) (enter 0. for unused parameters)
3.3) dx for grid [m]
3.4) dy for grid [m]
3.5) starting x value for grid [m]
3.6) starting y value for grid [m]
3.7) number of x grid points. The maximum number of x grid points is 100.
3.8) number of y grid points. The maximum number of y grid points is 5000.
3.9) file # for field output on the grid (or 0 for none) {20-99}
The format of the output file generated by parameter 9 is listed in section 5.2.
3.12) radius of ring [m]
3.13) cross sectional radius of bent rod [m]
3.14) total current [A]
3.15) Bdipole superimposed dipole field [ T ]
This command uses the same grid arrays as the r-z commands.
(Command parameters continued)
(3) x-y-s grid
1) grid number (I) {1}
2) field type (A4) { STUS }
3) field parameters (R) (enter 0. for unused parameters)
3.2) file # of input 3D field values or spline coefficients {20-99}
See file formats under STUS.
3.3) curvature flag
0: straight grid
1: curved grid
3.4) reference momentum [GeV/c]
3.5) field scaling factor Set to 1.0 for no scaling.
3.8) curvature sign flag
if parameter=1 => flip sign of HREF in input file
3.9) file format flag
0: formatted B grid
1: unformatted B grid
2: unformatted spline coefficients of B grid
For a curved grid (parameter 3.3 = 1): if href in the input file is not 0, then href is used as the constant curvature; if href in the input file is 0, then pref is used with the local Bx and By on-axis fields to determine the curvature.
3.10) Longitudinal shift parameter. If a longitudinal grid index JZ is entered here, the field grid stored in memory starts at JZ, wraps through the beginning of the grid and ends at longitudinal index JZ-1.
(Command parameters continued)
1.1) REFPAR (I) Use BMTYPE particle code to specify reference particle type. {1 - 5}
1.2-1.4) see below
1.5) PHMODREF (I) phase model
2: uses iterative procedure to find 0-crossing phase; tracks thru all regions; only works with ACCEL models 1, 2 and 13.
3: assumes constant reference particle velocity
4: takes into account energy loss in absorbers and gain in cavities
5: allows quadratic energy change in cavities
6: allows quadratic energy change for any region
1.1) REFPAR2 (I) Use BMTYPE particle code to specify reference particle type {1-5}
1.2-1.4) see below
n.b. when using the REF2 command in conjunction with ACCEL model 10, the momentum of the two reference particles should be different.
The meaning of parameters 1.2 – 1.4 in REFP and REF2 depend on the value of PHMODREF according to the following table.
|
PHMODREF |
2 |
3 |
4 |
5 |
6 |
|
1.2 = |
- |
pZ0 |
pZ0 |
E0 |
E0 |
|
1.3 = |
- |
t0 |
t0 |
dE/dz |
dE/dz |
|
1.4 = |
- |
- |
dE/dz |
d2E/dz2 |
d2E/dz2 |
|
app |
RF only |
any region |
RF only |
RF only |
any region |
The units are pZ0 [GeV/c], E0 (total
energy) [GeV], t0 [s], dE/dz [MeV/m], and d2E/dz2 [MeV/m2].
If a command has t0, pZ0 or E0 set to 0., the corresponding quantity keeps its
existing value.
(Command parameters continued)
REPEAT
1) NREP (I) # of times to repeat following region commands
RKICK
1.1) field type (A4) {SOL, DIP, HDIP, QUAD, SQUA, SEX; SCAL}
1.2) mean strength (R) integrated multipole strength [ T / mn * m ]
1.3) σ (strength) (R) [ T / mn * m ]
1.4) coupling parameter (R)
1.5) azimuth or length (R)
This generates a random momentum kick based on the magnetic field configuration given in field type. The output of this command can be given for longitudinal fields (SOL) and transverse fields independently. The SCAL field type is used to scale the strengths of all following RKICK commands. In this case the 2nd parameter is a scaling factor for the mean values and the 3rd parameter is a scaling factor for the standard deviations, as follows.
SCAL mean_factor sigma_factor 0. 0.
The coupling parameter can be used to correlate RKICK commands. This parameter can have the following four values.
0: generate a random value
1: generate a random value and save it
2: used the saved random value
3: used the saved random value with the opposite sign
One value can be saved for longitudinal kicks and one value
can be saved for transverse kicks. For solenoidal fields the 5th
parameter is the solenoid length in meters. For transverse fields the 5th
parameter determines the azimuthal angle around the beam direction in which the
kick takes place. If the 5th parameter = -1, the kick direction is
chosen randomly from a uniform distribution. Otherwise the kick direction is
determined by the field type. The coupling parameter is also used here to
correlate kick directions. The random kicks are only computed for NSECTIONS =
1. When NSECTIONS > 1 the same kick
is applied at some given location as its kick for NSECTIONS = 1. There can be a
maximum of 100 RKICK commands in a job.
(Command parameters continued)
ROTATE
1.1) ANGLE (R) Rotation angle [degrees]
1.2) axis (I) {1,2,3}
1: x
2: y
3: z
1.3) apply to (I) {0,1,2}
0: all particles
1: reference particle only
2: normal particles only
This command can be used to make vertical bends, e.g.
ROTATE
! switch x and y coordinates
90. 3. 0.
SREGION
! usual horizontal bend region
...........
ROTATE
! switch x and y coordinates back
-90.
3. 0.
SREGION
1.1) SLEN (R) Length of this s region [m]
1.2) NRREG (I) # of radial subregions of this s region {1-4}
1.3) ZSTEP (R) step for tracking particles [m]
Note that for fixed-stepping the program may modify this value slightly to get an integral number of steps in the region.
(following repeated for each r subregion)
2.1) IRREG (I) r-region number
2.2) RLOW (R) Inner radius of this r subregion[m]
2.3) RHIGH (R) Outer radius of this r subregion[m]
3) FTAG (A4) Tag identifying field in this r subregion
(see specific field type below)
4) FPARM (R) 15 parameters describing field(see specific field type below)
These 15 parameters must be on one input line.
5) MTAG (2A4) Tag identifying
material composition in this r subregion
The wedge geometry can accept a second MTAG parameter. The
first material refers to the interior of the wedge. The second material, if
present, refers to the exterior of the wedge. If a second MTAG parameter is not
present, vacuum is assumed. (see specific material type below)
6) MGEOM (A6) Tag identifying material geometry in this r subregion.
(see specific material type below)
7) GPARM (R) 10 Parameters describing material geometry.
These 10 parameters must be on one input line.
(see specific material type below)
(Command parameters continued)
1.1) NCELLS (I) number of consecutive following cells with tapered parameters
This command must be used in conjunction with BLOCK(4) or BSOL(5).
TILT
1.1) PSI (R) σ of tilt angle distribution [deg]
1.2) PHI (R) angle of rotation w.r.t. x axis in x-y plane [deg]
If PHI = -1 => angle of rotation axis is chosen randomly from a uniform distribution.
TRANSPORT
1) 1st row of transport matrix (variables x, x', y, y', d(length), dp/p )
2) 2nd row of transport matrix,......
6) 6th row of transport matrix
You must define a reference particle in order to use this command.
4. Field, material and geometry parameters
Enter FTAG in UPPER case. Unused parameters should be set to 0.
NONE drift in field free region
( set all parameters to 0 )
ACCE(L) linear accelerator fields
1 model
1: EZ only with no transverse variation
2: cylindrical TM01p pillbox resonator
3: traveling wave cavity
4: approximate fields for symmetric circular-nosed cavity
5: user-supp
6: induction linac model - waveform from user-supplied polynomial coefficients
7: induction linac model - internally generated waveform
8: induction linac model - waveform from user-supplied file
9: sector-shaped pillbox cavity (circular cross section)
10: variable {frequency, gradient} pillbox cavity
11: straight pillbox or SuperFish cavity in dipole region
12: sector-shaped pillbox cavity (rectangular cross section)
13: open cell standing wave cavity
The initial phase parameter can be used for any PHASEMODEL and ACCEL models 1-5.
For model = 1
2 frequency [MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 parameter to approximate a rectangular cavity in cylindrical geometry; if set to radius of curvature ρ, then EZ is scaled by 1-x/ ρ, where x is the horizontal distance from the reference circle.
6 (not used)
7 (not used)
8 mode
0 : time-independent
1: sinusoidal time variation
For model = 2
2 frequency f [MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 parameter to approximate a rectangular cavity in cylindrical geometry; if set to radius of curvature ρ, then the field components are scaled by 1-x/ ρ, where x is the horizontal distance from the reference circle.
6 x offset of cavity [m]
7 y offset of cavity [m]
8 longitudinal mode p {0,1}
For mode = 0 Rcav = 0.383 * λ
For mode = 1 Rcav = 2.405 / {(2 π f)2 - (π /SLEN)2 }1/2
For model = 3
2 frequency f [MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 (not used)
6 (not used)
7 (not used)
8 phase velocity of RF wave βW . {0 < βW < 1}
For model = 4
2 frequency [MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 (not used)
6 (not used)
7 (not used)
8 total length of cavity [m]
9 total gap [m]
10 radius of drift tube [m]
11 radius of nose piece [m]
For model = 5
2 frequency[MHz]
4 phase shift [deg] {0-360}.
8 file ## of azimuthally symmetric RF input file (see below) {20-99}
9 field strength normalization factor [MV/m] This multiplies the value in the SuperFish file.
10 radial cutoff for cavity [m]
11 axial distance from start of region to center
12 axial symmetry through center of cavity
0: symmetric
1: not symmetric
The contents of the user-supp
1.1 zmin Start of axial grid [cm]
1.2 zmax End of axial grid [cm]
1.3 Nz # of z grid points {<151}
2 frequency [MHz]
3.1 rmin Start of radial grid [cm]
3.2 rmax End of radial grid [cm]
3.3 Nr # of r grid points {<151}
for ir=1,Nr
for iz=1,Nz
4.1 Ez axial electric field [MV/m]
4.2 Er radial electric field [MV/m]
4.3 E magnitude of electric field [MV/m]
4.4 Hphi azimuthal magnetic field [A/m]
next iz
next ir
The grids should extend beyond the region where tracking will occur.
For model = 6
2 time offset from start of voltage pulse[s]
3 accelerator gap [m]
4 time reset parameter (see below)
5 V0 term in polynomial expansion of voltage pulse [V ]
6 V1 term in polynomial expansion of voltage pulse [V / μs]
7 V2 term in polynomial expansion of voltage pulse [V / μs^2]
8 V3 term in polynomial expansion of voltage pulse [V / μs^3]
9 V4 term in polynomial expansion of voltage pulse [V / μs^4]
10 V5 term in polynomial expansion of voltage pulse[V / μs^5]
11 V6 term in polynomial expansion of voltage pulse[V / μs^6]
12 V7 term in polynomial expansion of voltage pulse[V / μs^7]
13 V8 term in polynomial expansion of voltage pulse[V / μs^8]
This model generates an EZ field across the accelerator gap. The field is time dependent, but does
not depend on z or r. The radial electric field and azimuthal magnetic fields are assumed to be
negligible. When the time reset parameter is 1, the start time for the voltage pulse is determined
from the time the reference particle entered the cell. The user can adjust this time using
parameter #2 above. Subsequent cells should use parameter #4 set to 0 to sample later portions of the same voltage pulse. A new pulse shape can be started at any time by setting parameter #4
back to 1.
For model = 7
2 number of gaps
3 starting voltage [GV]
4 voltage swing [GV]
5 time offset [s]
6 target kinetic energy [GeV]
7 pulse duration [s]
8 parameter to adjust slope at end of voltage pulse
9 number of bins in voltage pulse
10 gap length [m]
11 file # of output diagnostic file {20-99} (Set this <20 for no diagnostic output.)
12 kill particle flag (Set=1 to eliminate non-useful particles)
13 restart flag (Set =1 to restart calculation)
For model = 8
2 time offset from start of voltage pulse[s]
3 accelerator gap [m]
4 time reset parameter [s](see below)
5 file number of waveform input (see format below) {20-99}
6 polynomial interpolation order, 1=> linear, 2=>quadratic, etc. {1-3}
7 file # for output diagnostic file (see format below){20-99}
8 time increment between diagnostic outputs to file [s]
This model generates an EZ field across the accelerator gap. The field is time dependent, but does
not depend on z or r. The radial electric field and azimuthal magnetic fields are assumed to be
negligible. The gap parameter is used to convert the voltage profile into an electric field. The field is applied everywhere in the region.
When the time reset parameter is 1, the start time for the voltage pulse is determined
from the time the reference particle entered the cell. The user can adjust this time using
parameter #2 above. Subsequent cells can use parameter #4 set to 0 to sample later portions of
the same voltage pulse. A new pulse shape can be started at any time by setting parameter #4
back to 1.
The contents of the waveform input file FOR0##.DAT is
1) number of points N {1-100}
This is followed by N pairs
2) t(i) V(i) [s] [V]
An output diagnostic file is initialized for an induction linac region where the time reset
parameter=1 and parameter 7 above is in the range {20-99}. Output occurs when the elapsed
time from the previous output exceeds the increment given in parameter 8. Output continues for
subsequent induction linac regions provided parameter 7 remains in the specified range. The
contents of the file are
1) column id header
2) region particle z t Ez
For model = 9
2 frequency f[MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
For model = 10
2 (not used)
3 (not used)
4 phase shift [deg] {0-360}.
5 number of wavelengths separating the two reference particles
6 reset parameter (see below)
7 Total length L of buncher [m]
8 g0 [MV/m]
9 g1 [MV/m]
10 g2 [MV/m]
11 (not used)
12 phase model
0: 0-crossing time set by tREFP
1: 0-crossing time set by ½ * (tREFP + t REF2)
This model uses a TM010 mode pillbox cavity. It can only be used with REFP and REF2 defined and phasemodel=2,3,4. The cavity frequency is set using the number of wavelengths (parameter 5) and the time difference between the two reference particles. When the reset parameter is 1, the starting location of the buncher is determined from the current position of the reference particle. Subsequent ACCEL commands should use parameter #6 set to 0 to sample later portions of the gradient waveform, which is given by
G = g0 + g1*(z/L) + g2*(z/L)^2
A new pulse shape can be started at any time by setting parameter #6 back to 1.
For model = 11
2 frequency f [MHz]
3 gradient on-axis at center of gap for a pillbox cavity [MV/m]
4 phase shift [deg] {0-360}.
5 radial offset of center of cavity from reference trajectory [m]
6 axial length of cavity [m] If this entered as 0, the program computes the largest pillbox cavity that fits in the sector shaped region
7 cavity type
0: pillbox
1: SuperFish
8 file ## of azimuthally symmetric SuperFish RF input file (see model 5) {20-99}
9 SuperFish field normalization [MV/m] This multiplies the value in the SuperFish file.
10 SuperFish radial cut off [m]
11 axial displacement of center of SuperFish cavity from start of the region [m]
12 SuperFish axial symmetry
0: symmetric
1: not symmetric
For model = 12
2 frequency f[MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 radial offset of center of cavity from reference trajectory [m]
6 cavity width [m]
7 cavity height [m]
For model = 13
2 frequency f [MHz]
3 gradient on-axis at center of gap [MV/m]
4 phase shift [deg] {0-360}.
5 flag for hard edge focusing
0: both entrance and exit focusing
1: exit focusing only
2: entrance focusing only
3: no edge focusing
BLOCK field made up from sum of fields from annular solenoidal current blocks
1 model
1: exact field from single block
2: exact field from sum of blocks in data file
3: interpolate data file field points from predefined grid
4: interpolate data file field points from blocks with tapered currents
For CELL fields repetition of a cell uses the same external file over and over. A new cell block
can use a different external file.
For model = 1
2 z offset of center of block from start of region [m]
3 inner radius of block [m]
4 outer radius of block [m]
5 length of block [m]
6 current density [A / mm^2]
7 algorithm
0: from numerical integration
1: from series
For model = 2
2 file ##of block input (see below) {20-99}
3 algorithm
0: from numerical integration
1: from series
11 current density scaling factor
If the file number is entered as a negative number, the current densities in the external file are all
reversed in polarity.
The contents of the block data input file FOR0##.DAT is
1 title (a80)
2 NBLOCKS {1-1000}
( 3 repeated for each block)
3.1 block #
3.2 relative z offset of this block [m]
3.3 length of block [m]
3.4 inner radius of block [m]
3.5 outer radius of block [m]
3.6 current density [A / mm^2]
For model = 3
2 grid ##of block field {1-4}
3 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
For model = 4
2 file number of block data {20-99} The file format is described under model 2.
3 grid dz [m]
4 grid dr [m]
5 total length of grid in z [m]
6 total length of grid in r [m]
7 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
8 algorithm
0: from numerical integration
1: from series
9 file number of taper current data {20-99}
10 number of r-z grid that contains the calculated field {1-4}
This feature assumes a solenoid lattice like Study 2, i.e. two symmetric “focusing” coils and a “coupling” coil in each cell. It also assumes that the block data file contains information on the two cells before and the two cells after the actual cell of interest in order to get the correct boundary conditions. Thus there should be 15 blocks in the input file.
The format of the tapered current input file FOR0##.DAT is
1 title (a80)
2 ntaper number of cells that follow {1-200}
(3 repeated for each cell)
3.1 cell #
3.2 focus coil current density [A/mm2]
3.3 coupling coil current density [A/mm2]
BROD field from bent axial current rod
1 model
1: interpolate data file field points from predefined grid
For model = 1
2 grid ##of block field {1-4}
10 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
12 R, radius of ring [m]
The bent rod field must first be stored in an array with the GRID command. The curvature used for tracking is 1 / R. The parameters here and in the associated GRID command should obey the constraint
1 / R = e / pREF * BDIP
BSOL bent solenoid
1 model
1: hard edge dependence for Bs and By
2: soft edge dependence for Bs, By and g using dTANH(s)
3: user-supplied fields on-axis
4: user-supp
5: tapered lattice cells
For model = 1
2 peak value of Bs [T]
3 peak value of By [T]
4 curvature factor
1: use curvature from parameter 7
2: use local BY on axis and pREF
5 reference momentum, pREF [GeV/c]
6 quad component of dipole field [T/m]
7 curvature [ m-1 ]
Hard-edge field models can include the focusing effects of the missing fringe field by using EDGE commands before and after the hard-edge field region.
For model = 2
2 peak value of Bs [T]
3 peak value of By [T]
4 quad component of dipole field [T/m]
5 reference momentum, pREF [GeV/c]
6 central length of solenoid [m]
7 end length of solenoid [m]
8 attenuation length of solenoid [m] {>0}
9 central length of dipole and quad [m]
10 end length of dipole and quad [m]
11 attenuation length of dipole and quad [m]
12 constant offset for Bs [T]
13 curvature factor
1: use curvature from parameter 14
2: use
local BY on axis and pREF
14 curvature [ m-1 ]
15 order of expansion
{1-3}
The attenuation lengths (parameters 8 and 11) must be entered, even if the strength is 0.
For model = 3
2 file # of user-supplied input (see contents below) {20-99}
3 reference momentum, pREF [GeV/c]
4 curvature in horizontal plane, h [ m-1 ]
5 curvature factor
1: use curvature from parameter 4
2:
use local BY on axis and pREF
3: take h(s) from input file
6 scale factor for BS
7 scale factor for BY
8 scale factor for b1
9 scale factor for b2
10 scale factor for b3
11 scale factor for b4
12 scale factor for b5
13 scale factor for a0
14 scale factor for h
15 order of calculation {1-5}
The contents of the input file FOR0##.DAT of on-axis field multipoles is
1 title (a80)
2 # of points {1-2000}
(3, repeated for each point)
3.1 s [m]
3.2 BS [T]
3.3 b0 [T]
3.4 b1 [T/m]
3.5 b2 [T/m2]
3.6 b3 [T/m3]
3.7 b4 [T/m4]
3.8 b5 [T/m5]
3.9 a0 [T]
3.10 h [ m-1 ]
The s grid should start at 0. Make the s grid at least 1 grid spacing longer than the actual size of
the cell (or the field will be 0 at the boundary points). The off-axis fields can be calculated at up to 5th order in the transverse coordinates. Set the scale factors of unused multipoles to 0 to speed up execution.
For model = 4
2 file # of user-supplied input (see contents below) {20-99}
3 reference momentum, pREF [GeV/c]
4 order of field calculation {1-5}
5 curvature factor
1: use curvature from parameter 15
2:
use local BY and BX on axis and pREF
6 scale factor for solenoid field strength
7 scale factor for b0 field strength
8 scale factor for a0 field strength
9 scale factor for b1 field strength
10 scale factor for a1 field strength
11 scale factor for b2 field strength
12 scale factor for a2 field strength
13 scale factor for b3 field strength
14 scale factor for a3 field strength
15 curvature, h [ m-1 ]
The sign of h in parameter 15 should correspond to the dipole field. The 5th order calculation does not contain terms for bending out of the midplane. The multipole expansion for BY on the midplane is
BY = b0 + b1 x + b2
x2 + b3 x3 + b4 x4 + b5
x5
Set the scale factors of unused quad and higher multipoles to 0 to speed up execution.
The contents of the input file FOR0##.DAT for model 4 is
1 title (a80)
2.1 period [m]
2.2 field strength for solenoid component [T]
2.3 field strength for b0 component [T] (normal dipole term)
2.4 field strength for a0 component [T] (skew dipole term, etc.)
2.5 field strength for b1 component [T/m]
2.6 field strength for a1 component [T/m]
2.7 field strength for b2 component [T/m2]
2.8 field strength for a2 component [T/m2]
2.9 field strength for b3 component [T/m3]
2.10 field strength for a3 component [T/m3]
2.11 field strength for b4 component [T/m4]
2.12 field strength for a4 component [T/m4]
2.13 field strength for b5 component [T/m5]
2.14 field strength for a5 component [T/m5]
3 maximum Fourier order {0-199}
4 2 nd title (a80)
(5 repeated for each order)
5.1 m order #
5.2 cm coefficient for solenoid field
5.3 dm coefficient for solenoid field
5.4 cm coefficient for b0 field
5.5 dm coefficient for b0 field
5.6 cm coefficient for a0 field
5.7 dm coefficient for a0 field
5.8 cm coefficient for b1 field
5.9 dm coefficient for b1 field
5.10 cm coefficient for a1 field
5.11 dm coefficient for a1 field
…
5.26 cm coefficient for a5 field
5.27 dm coefficient for a5 field
The form of the Fourier series used for each multipole component is
f (s) = S ( cm COS(u) + dm SIN(u) )
where u = 2πms / λ.
For model = 5
2
file # of user-supp
3 reference momentum, pREF [GeV/c]
4 order of field calculation {1-5}
5 curvature factor
1: use curvature from parameter 15
2:
use local BY and BX on axis and pREF
6 file # of tapering profile (see contents below) {20-99}
7 file # of taper diagnostics {20-99}
15 curvature, h [ m-1 ]
The file format for the tapering profile is
1. title (a80)
2. number of tapered cells (I) {<301}
3.1 cell # (I)
3.2 taper factor (R)
Repeat 3 for each tapered cell.
This model must be used as a cell field. It works in
conjunction with the TAPER command. If f is the taper factor for a given cell,
then the multipole strengths and RF frequencies are multip
COIL field made up from sum of fields from circular current loops
1 model
1: exact field from single loop
2: exact field from sum of loops in data file
3: interpolate data file field points from predefined grid
Models 2 and 3 can be used as CELL fields. Repetition of a cell uses the same external
file over and over. A new cell block can use a different external file.
For model = 1
2 z offset of the coil from start of region [m]
3 radius a of coil [m]
4 currentI [A]
Baxis = mu_o I / 2a = 2 pi 10^-7 I / a
For model = 2
2 file ##of coil input (see below) {20-99}
If the file number is entered as a negative number, the current densities in the external file are all
reversed in polarity.
11 current density scaling factor
For model = 3
2 grid ##of coil field {1-4}
3 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
The contents of the coil input data file FOR0##.DAT is
1 title (a80)
2 NCOILS {1-1000}
( 3-6repeated for each coil)
3 coil #
4 relative z offset of this coil [m]
5 radius of coil[m]
6 current[A]
DIP vertical sector dipole field
1 model
1: hard-edge dipole + multipole fields (2nd order)
2: dTANH(s) BY with higher multipoles (3rd order)
3: hard-edged combined function dipole
4: hard-edge dipole with adjustable pole face angles
For model = 1
2 dipole field strength [T]
3 (not used)
4 reference momentum [GeV/c]
5 quad strength [T/m]
6 sextupole strength [T/m^2]
Hard-edge field models can include the focusing effects of the missing fringe field by using EDGE commands before and after the hard-edge field region.
For model = 2
2 dipole field strength [T]
3 curvature factor
h = 1 / ρgeom [ m-1]
0. => use local BY and BX on axis
4 reference momentum [GeV/c]
5 dipole central length [m]
6 dipole end length [m]
7 dipole end attenuation length[m]
8 quadrupole field component [T / m]
9 sextupole field component [T / m^2]
10 quadrupole central length [m]
11 quadrupole end length [m]
12 quadrupole end attenuation length [m]
13 sextupole central length [m]
14 sextupole end length [m]
15 sextupole end attenuation length[m]
The sign of h in parameter 3 should correspond to the sign of the dipole field.
For model = 3
2 dipole field strength, b0 [T]
3 field index, n
4 reference particle momentum, pREF [GeV/c]
5 distance from machine center to reference circle, r0 [m]
6 curvature factor
h = 1 / ρgeom [ m-1]
0. => use local BY and BX on axis
7 parameter for reverse-bend magnets; set to 0 for normal sector magnets; set to 1 for radial sector magnets with center on same side as positive bend sectors.
The combined function dipole has a vertical field on axis given by
Byo = bo {ro / r}n
This model uses 8th order expansions in y/R to get the total Bx and By field components. The field is uniform in s. For FFAG magnets n is negative and the radius of curvature of the particle = pREF / (q bo ) is smaller than r0 .
For model = 4
2 dipole strength [ T ]
3 (not used)
4 reference momentum [GeV/c]
5 (not used)
6 (not used)
7 axial center position of dipole from start of region [m]
8 half axial length of dipole along reference trajectory [m]
9 entrance pole rotation angle [deg]
10 exit pole rotation angle [deg]
11 horizontal half width of aperture [m]
12 vertical half width of aperture [m]
A positive pole rotation angle means the edge closest to the center of curvature is decreased by the rotation (TRANSPORT convention). It is up to the user to be sure that the region length extends out as far as the rotated pole faces. Otherwise they will be truncated longitudinally.
1 model
1: static
For model = 1
2 EX [V/m]
3 EY [V/m]
4 EZ [V/m]
5 xmin [ m ]
Bounding box for field
6 xmax [
m ]
7 ymin
[m]
8 ymax
[m]
9 zmin
[m]
10 zmax
[m]
11 C, curvature factor
0: respect curvature
1: force rectangular
2: specify curvature
3: specify curvature and force rectangular
12 curvature [m^-1] for C=2,3 in parameter #11
FOFO solenoidal FOFO lattice element
1 model
1: linear end ramp in Bz(Br from div B = 0)
2: sinusoidal Bz with Bessel radial dependence
For model = 1
2 bmag [T] (amplitude of varying Bz)
3 bcen [T] (central offset value of varying Bz)
4 period [m]
5 offset from beginning of the cell or region [m]
offset = 0, Bz starts at bcen, rises to bmag at a quarter period, ...
offset=-period/4, Bz starts at bmag, falls to bcen at a quarter period,...
For model = 2
2 bmag [T] (amplitude of varying Bz)
3 bcen [T] (central offset value of varying Bz)
4 period [m]
5 offset from beginning of the cell or region [m]
offset = 0 starts at bcen
HDIP horizontal sector dipole field
1 model
1: hard-edge skew dipole plus multipoles (2nd order)
2: dTANH(s) BX with higher multipoles
For model = 1
2 a0 dipole field strength [T]
3 (not used)
4 reference momentum [GeV/c]
5 a1 quad strength [ T/m ]
6 a2 sextupole strength [ T/m2 ]
Hard-edge field models can include the focusing effects of the missing fringe field by using EDGE commands before and after the hard-edge field region.
For model = 2
2 dipole field strength [T]
3 (not used)
4 reference momentum [GeV/c]
5 dipole central length [m]
6 dipole end length [m]
7 dipole end attenuation length[m]
8 quadrupole field component [T / m]
9 sextupole field component [T / m^2]
10 quadrupole central length [m]
11 quadrupole end length [m]
12 quadrupole end attenuation length [m]
13 sextupole central length [m]
14 sextupole end length [m]
15 sextupole end attenuation length[m]
HELI(X) helical field
1 model
1: simple rotating dipole
2: infinite he
3: multi-filar helical multipoles
4: user-supp
5: he
6: he
Models 2-5 are only defined here for particle radius less
than the radius of the he
For model = 1
2 dipole field strength [T]
3 helix period [m]
4 dipole entrance and exit taper length [m]
8 start value of solenoid field [T]
9 central value of solenoid field [T]
10 end value of solenoid field [T]
11 solenoid entrance taper length, L1 [m]
12 solenoid central length, L2 [m]
13 solenoid exit taper length, L3 [m]
14 reset parameter Set to 1 to reset accumulated helix length.
The total length of the helix must be L1+L2+L3.
For model = 2
2 current [A]
3 helix radius [m]
4 helix period [m] Cannot be 0. The sign gives the orientation of the twist.
5 starting azimuthal orientation [degrees]
6 (not used)
7 entrance and exit taper length for transverse field [m]
8 start value of solenoid field [T]
9 central value of solenoid field [T]
10 end value of solenoid field [T]
11 solenoid entrance taper length, L1 [m]
12 solenoid central length, L2 [m]
13 solenoid exit taper length, L3 [m]
14 reset parameter Set to 1 to reset accumulated helix length.
15 number of terms in series expansion
The total length of the he
(HELIX continued)
For model = 3
2 helix radius [m]
3 helix period [m] Cannot be 0. The sign gives the orientation of the twist.
4 dipole strength [ T ]
5 quadrupole strength [ T / m ]
6 sextupole strength [ T / m2 ]
7 entrance and exit taper length for transverse field [m]
8 start value of solenoid field [T]
9 central value of solenoid field [T]
10 end value of solenoid field [T]
11 solenoid entrance and exit taper length, L1 [m]
12 solenoid central length, L2 [m]
13 octupole strength [ T / m3 ]
14 reset parameter Set to 1 to reset accumulated helix length.
15 number of terms in series expansion
The total length of the helix must be 2*L1+L2. The solenoid field can be non-symmetric, but the transverse field tapering is done symmetrically.
For model = 4
2 file # of user-supplied multipoles {20-99}
3 reference radius ro [m]
4 helix period [m] Cannot be 0. The sign gives the orientation of the twist.
5 starting azimuthal orientation [degrees]
6 reference magnetic field, BREF [ T ]
7 entrance and exit taper length for transverse field [m]
8 start value of solenoid field [T]
9 central value of solenoid field [T]
10 end value of solenoid field [T]
11 solenoid entrance taper length, L1 [m]
12 solenoid central length, L2 [m]
13 solenoid exit taper length, L3 [m]
14 reset parameter Set to 1 to reset accumulated helix length.
1 title (a80)
2 number of supplied moments {1-20}
( Bn(i), An(i) ), i=1, Nmoments
For model = 5
2
file # of user-supp
3 (not used)
4 reference magnetic field, BREF [ T ]
5 reference radius ro [m]
6 scale factor for solenoid field strength
7 scale factor for b0 field strength
8 scale factor for a0 field strength
9 scale factor for b1 field strength
10 scale factor for a1 field strength
11 scale factor for b2 field strength
12 scale factor for a2 field strength
13 scale factor for b3 field strength
14 scale factor for a3 field strength
15 maximum multipole order to use {1 – 6}
Set the scale factors of unused multipoles to 0 to speed up execution.
The helical fields are given by T. Tominaka et al, NIM A 459:398 (2001), eq. 40. For example the radial magnetic field is
![]()
where In is a modified Bessel function and
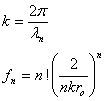
In principle each multipole can have its own axial period.
However, for a normal he
(HELIX continued)
The contents of the input file FOR0##.DAT for model 5 is
1 title (a80)
2 period of lattice cell, λ [m]
3.1
period of 0th order he
3.2
period of 1st order he
3.3
period of 2nd order he
3.4
period of 3rd order he
3.5
period of 4th order he
3.6
period of 5th order he
4.1 field strength for solenoid component [T]
4.2 field strength for b0 component [T] (normal dipole term)
4.3 field strength for a0 component [T] (skew dipole term, etc.)
4.4 field strength for b1 component [T/m]
4.5 field strength for a1 component [T/m]
4.6 field strength for b2 component [T/m2]
4.7 field strength for a2 component [T/m2]
4.8 field strength for b3 component [T/m3]
4.9 field strength for a3 component [T/m3]
4.10 field strength for b4 component [T/m4]
4.11 field strength for a4 component [T/m4]
4.12 field strength for b5 component [T/m5]
4.13 field strength for a5 component [T/m5]
5 maximum Fourier order {0-199}
6 2 nd title (a80)
(6 repeated for each order)
6.1 m order #
6.2 cm coefficient for solenoid field
6.3 dm coefficient for solenoid field
6.4 cm coefficient for b0 field
6.5 dm coefficient for b0 field
6.6 cm coefficient for a0 field
6.7 dm coefficient for a0 field
6.8 cm coefficient for b1 field
6.9 dm coefficient for b1 field
6.10 cm coefficient for a1 field
6.11 dm coefficient for a1 field
…
6.26 cm coefficient for a5 field
6.27 dm coefficient for a5 field
The form of the Fourier series used for each he
f (s) = S ( cm COS(u) + dm SIN(u) )
where u = 2πms / λ.
You must enter non-zero periods for all multipoles up to the highest order used in the calculations.
For model = 6
2 file # of user-supp
3 order of calculation {1-3}
4 he
5 he
1 title (a80)
2 number of axial points {1-2000}
3.1 s [m]
3.2 BS [T]
3.3 a0 [T]
3.4 b0 [T]
3.5 a1 [T/m]
3.6 b1 [T/m]
3.7 a2 [T/m2]
3.8 b2 [T/m2]
3.9 a3 [T/m3]
3.10 b3 [T/m3]
HORN magnetic (toroidal-like) horn
1 model
1: simple analytic model
2: sheet(s) with user-supp
For model = 1
2 minimum polar angle [deg]
3 maximum polar angle [deg]
4 current [ A ]
For model = 2
2 number of horn sheet files to read in {1,2}
3 current sca
4 input file # of first sheet {20-99} (see format below)
5 input file # of second sheet {20-99} (see format below)
6 radial boundary between sheets [m]
The contents of the input file FOR0##.DAT is
1 title (a80)
2 current (R) [A]
3 npoints (I) {1-50}
4 (i,
n.b. Up to two radially-displaced horn sheets can be active at one time. The z positions in the file are measured relative to the start of the region or cell.
KICK kickers and deflection cavities
1 model
1: TM210 rectangular deflection cavity
2: time-dependent transverse kicker
For model = 1
2 frequency [MHz]
3 gradient [MV / m]
4 phase [deg] {0-360}
5 width [m]
The width must be > λ. The length is taken from SLEN; height is computed from eigenvalue equation.
For model = 2
2 input file #{20-99} (see format below)
3 time offset from start of pulse [s]
4 polynomial interpolation order {1-3}
5 azimuthal orientation of B, φ [deg]
6 magnitude of B, b0 [T]
7 slope, m {-1,1}
8 pulse width, τ [s]
9 B offset, boff [T]
If the input file number is in the range {20-99} the magnetic field pulse as a function of time is
taken from the input file. The input file should contain
# of following points
t [sec] b0 [T] for each point
If an input file is not given, the pulse is computed analytically using parameters 6-9.
b(t) = boff + b0 m t / τ
BX = b cos φ
BY = b sin φ
Times are measured relative to the time the reference
particle entres the kicker region.
QUAD quadrupole field
1 model
1: constant gradient over entire region (hard edge) (2nd order)
2: dTANH(s) quad with sextupole
For model = 1
2 gradient strength [T/m] (+:focus horizontal, -:focus vertical)
3: sextupole strength [T/m2]
For model = 2
2 gradient strength [T/m] (+:focus horizontal, -:focus vertical)
3 quad central length [m]
4 (not used)
5 quad end length [m]
6 quad end attenuation length [m]
7 sextupole strength [T/m2]
8 sextupole central length [m]
9 sextupole end length [m]
10 sextupole end attenuation length [m]
ROD axial current carrying rod
1 model level
1: Bphi only, constant in z, all other 0
2: level 1 + linear end fringe field
3: level 2 + minimal nonlinearity in radial dependence
4: dTANH(s) model for Bphi
5: tapered radius
For model = 1
2 Bphi [T] at outer radius(note that sign of B causes focus or defocus)
3 radius of rod [m]
For model = 2 or 3
2 Bphi [T] at outer radius(note that sign of B causes focus or defocus)
3 radius of rod [m]
4 length of central region[m]
5 length of end field region[m]
For model = 4
2 Bphi strength [T]
3 radius of rod [m]
4 central length [m]
5 end length [m]
6 end attenuation length [m]
For model = 5
2 Bc [T] (flat central field strength; sign is important!)
3 Rc [m] (flat central rod radius)
4 Lc [m] (central field length)
5 R1 [m] (starting rod radius)
6 L1 [m] (length of entrance transition region)
7 R2 [m] (ending rod radius; set to Rc to prevent /0)
8 L2 [m] (length of exit transition region; set to 0.01 to prevent /0)
SEX sextupole field
1 model
1: hard edge field (2nd order)
2: dTANH(s) sextupole strength (3rd order)
For model = 1
2 sextupole strength [T/m^2]
For model = 2
2 sextupole strength [T/m^2]
3 central length [m]
4 (not used)
5 end length [m]
6 end attenuation length [m]
SHEE(T) field made up from sum of fields from annular solenoidal current sheets
1 model
1: exact field from single sheet
2: exact field from sum of sheets in data file
3: interpolate data file field points from grid
4: interpolate data file field points from “moving” grid
5: interpolate field from predefined r-z grid
This field type is often used as a CELL field. Repetition of a cell uses the same external
file over and over. A new cell block can use a different external file.
For model = 1
2 z offset of left edge of sheet from start of region [m]
3 radius of sheet [m]
4 length of sheet [m]
5 current density [A-turns/m]
For model = 2
2 file ##of sheet input {20-99} See model 3 for file definition.
If the file number is entered as a negative number, the current densities in the external file are all
reversed in polarity.
11 current scaling factor
For backwards compatibility if this parameter is exactly 0, it is set to 1 by the program.
For model = 3
2 file ##of sheet input (see below) {20-99}
If the file number is entered as a negative number, the current densities in the external file are all
reversed in polarity.
3 grid dz [m] (# z grid points < 5000)
4 grid dr [m] ( # r grid points < 100 )
5 total z grid length [m]
6 total r grid length [m]
Make the z and r grids at least 1 grid spacing longer in each direction than the actual size of the
cell or the field will be 0 at the boundary points.
7 cutoff length in z for including sheets [m]
This is the distance between the present location of the particle and the start of a sheet, after
which you can ignore the sheet in the calculation. The intent is not to waste time calculating
sources that are very far away.
8 interpolation level
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
9 file ## of field output on the grid {20-99}
Set this <20 if you don't want the output file. The file format is given in section 4.2.
10 grid calculation suppression parameter{0,1}
Normally leave this set to 0. If it is set to 1, the fields on the grid will not be recomputed.
11 current scaling factor
For backwards compatibility if this parameter is exactly 0, it is set to 1 by the program.
Don't allow grid points to overlap sheet positions. A SHEET field using a grid cannot be
superimposed on a COIL or BLOCK field that also uses a grid.
The contents of the sheet data input file FOR0##.DAT is
1 title (a80)
2 NSHEETS {1-1000}
3 current scaling factor
( 4-8repeated for each sheet)
4 sheet #
5 relative z offset of this sheet[m]
6 length of sheet [m]
7 radius of sheet [m]
8 current density [A-turns/m]
The format of the output file generated by parameter 9 is listed in section 4.2.4.
For model = 4
2 file ## of field output on grid {20-99} Set this < 20 if you don’t want output file.
Format of file is described in sec. 5.2.4. Output is only written at the boundaries of grid partitions.
3 interpolation level
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
Use of this model requires the user to specify the control variables MAGCONF and MAPDEF.
The MAGCONF variable specifies the magnet configuration file with the following format.
1 title (a80)
2 # of following solenoid magnet descriptions (I) {1-1000}
(3- 9 repeated for each magnet)
3 id # (I) for user convenience
4 absolute z location of the start of this solenoid (R) [m]
5 length of solenoid (R) [m]
6 inner radius of solenoid (R) [m]
7 radial thickness of solenoid (R) [m]
8 current density (R) [A / mm^2]
9 # of sheets to use in calculating the field (I) {>1}
The coils in this file must be ordered by their starting z locations.
The MAPDEF variable specifies grid partition file to use in the simulation with the
following format.
1 title (a80)
2 # of following grid definitions (I) {1-100}
(3- 9 repeated for each grid)
3 id # (I) for user convenience
4 absolute z location of the start of the partition (R) [m]
5 axial step size of grid (R) [m]
6 # of axial grid points (I) {2-5000}
7 radial step size of grid (R) [m]
8 # of radial grid points (I) {2-100}
9 axial distance to start of solenoid coils within which coils should be used in field
calculations (R) [m]
When using this model the starting value of each partition must correspond with the starting location of an ICOOL region.
Make the z and r grids at least 1 grid spacing longer in each direction than the actual size of the
cell or the field will be 0 at the boundary points. You must include a reference particle with this model.
For model = 5
2 grid ##of sheet field {1-4}
3 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
4 z mode flag
0: use relative z positions (normal)
1: use absolute z positions (moving grid)
SOL solenoid field
1 model level
1: Bz with constant central region + linear ends
2: dTANH(z) Bz dependence
3: field from sum of circular current loops
4: field from annular current sheet
5: field from thick annular current block
6: interpolate field from predefined USER r-z grid
7: tapered radius
8: hard-edge with adjustable end fields
9: determine field from file of Fourier coefficients
10: determine field from file of on-axis field
For model = 1
2 field strength [T]
3 length of central region, CLEN[m] (You can use this to get a tapered field profile)
4 length of entrance end region, ELEN1 [m] This is the displacement of the
upstream end of the solenoid from the start of the region.
5 constant offset for Bz [T]
Use parameter 5 to get an indefinitely long, constant solenoidal field.
6 length of exit end region, ELEN2 [m].
For a symmetric field, set SLEN =CLEN + ELEN1 + ELEN2. Hard-edge field models can include the focusing effects of the missing fringe field by using EDGE commands before and after the hard-edge field region.
For model = 2
2 field strength [T]
3 length of central region, CLEN[m]
4 length for end region, ELEN [m] (This is the displacement of the
upstream end of the solenoid from the start of the region; for a symmetric field, set SLEN =
CLEN + 2*ELEN.)
5 order of vector potential expansion {1, 3, 5, 7}
6 end attenuation length, [m] (Set larger than maximum beam size)
7 constant offset for Bs [T]
For model = 3
2 field strength [T]
3 length of central region, CLEN[m] (This is the region over which the coils are
distributed)
4 length for end region, ELEN[m] (This is the displacement of the
upstream end of the solenoid from the start of the region; for a symmetric field, set SLEN =
CLEN + 2*ELEN.)
5 # of coils loops (equi-spaced over CLEN)
6 radius of coils [m]
For a symmetric field with 1 loop, set ELEN=0.5 SLEN.
For model = 4
2 field strength [T]
3 length of sheet [m]
4 z offset of center of sheet from start of region [m]
5 radius of sheet [m]
For model = 5
2 field strength [T]
3 length of block [m]
4 z offset of center of block from start of region [m]
5 inner radius of block [m]
6 outer radius of block[m]
For model = 6
2 grid ##of user-supplied field {1-4}
3 interpolation level {1-3}
1: bi-linear
2: bi-quadratic polynomial
3: bi-cubic polynomial
The required format of the field map is
title (A80)
# of z grid points (I) {1-5000}
# of r grid points (I) {1-100}
i, j, zi, rj, BZi,j, BRi,j (I, R)
For model = 7
2 Bc [T] (flat central field strength)
3 Rc [m] (flat central coil radius)
4 Lc [m] (central field length)
5 B1 [T] (starting field strength)
6 R1 [m] (starting coil radius)
7 L1 [m] (length of entrance transition region)
8 B2 [T] (ending field strength)
9 R2 [m] (ending coil radius)
10 L2 [m] (length of exit transition region)
This model applies a geometry cut on particles whose radius exceeds the specified radial taper.
For model = 8
2 BS [T]
3 flag on whether to include end focusing
0: both entrance and exit focusing
1: exit focusing only
2: entrance focusing only
3: no edge focusing
4 focusing deficit at entrance [T2 m]
5 focusing deficit at exit [T2 m]
The focusing deficit is B2L - ∫B2 ds. The deficit is independent of the focusing effect chosen with parameter 3.
For model = 9
2 file number JK for input data (I) File name is for0JK.dat
3 order of off-axis expansion (I) {1, 3, 5, 7}
4 scale factor (R) Multiplies field strength
The contents of the input file for0JK.dat is
1 title (A80)
2.1 period, λ (R)
2.2 field strength, S (R)
3 maximum Fourier order (I)
(4 repeated for each order)
4.1 order, m (I) {0 – 199}
4.2 cm (R)
4.3 dm (R)
The on-axis field is given by
f (s) = S S ( cm COS(u) + dm SIN(u) )
where u = 2πms / λ.
For model = 10
2 file number JK for input data (I) File name is for0JK.dat
3 order of calculation (I) {3,5,7}
4 scale factor (R) Multiplies field strength
The contents of the input file for0JK.dat is
1 title (A80)
2 number of points (I) {<1001}
3.1 z (R) [m]
3.2 Bz (R) [ T ]
SQUA skew quadrupole field
1 model
1: constant gradient over entire region (hard edge) (2nd order)
2: dTANH(s) quad only (3rd order)
For model = 1
2 gradient strength [T/m] (+:focus horizontal, -:focus vertical)
3 skew sextupole strength [T/m2]
For model = 2
2 gradient strength [T/m] (+:focus horizontal, -:focus vertical)
3 central length [m]
4 (not used)
5 end length [m]
6 end attenuation length [m]
STUS User supplied, static 3D magnetic field grid
1 model level
1: set up 3D grid at this location in ICOOL command stream
2: use 3D grid predefined with GRID command
For model = 1
2 file ## of input field grid (see below) {20-99}
3 curvature flag
0: straight grid
1: curved grid
4 reference momentum( pref ) [GeV/c]
5 field strength normalization factor (R)
6 interpolation model {0-3}
0: simple linear
1: spline (requires a spline input file, not a field grid!)
2: quadratic polynomial
3: cubic polynomial
7 grid calculation suppression parameter{0,1}
Normally leave this set to 0. If it is set to 1, the fields on the grid will not be recomputed.
8 curvature sign flag if parameter=1 => flip sign of HREF in input file
9 file format flag
0: formatted B grid
1: unformatted B grid
2: unformatted spline coefficients of B grid
10) Longitudinal shift parameter. If a longitudinal grid index JZ is entered here, the field grid stored in memory starts at JZ, wraps through the beginning of the grid and ends at longitudinal index JZ-1.
This command can also be used to input a user-supplied field to a background field definition. It is used as a field type argument for the BFIELD command.
For model = 2
2 interpolation model {0-3}
0: simple linear
1: spline
2: quadratic polynomial
3: cubic polynomial
3 curvature flag
0: straight grid
1: curved grid
The grid points must be equally spaced in a given direction. For BACKGROUND fields the value of MXG must agree with the parameter NXBKG of the BACKGROUND command, etc.
For a curved grid (parameter 3 = 1): if href in the input file is not 0, then href is used as the constant curvature; if href in the input file is 0, then pref is used with the local Bx and By on-axis fields to determine the curvature.
For file formats 0 and 1 the contents of the user supplied field file FOR0##.DAT is
title (a80)
mxg (I) number of x grid points {<101}
myg (I) number of y grid points {<101}
mzg (I) number of z grid points {<501}
href (R) curvature [m-1]
(xgr(i),i=1,mxg) (R) x grid points [m]
(ygr(i),i=1,myg) (R) y grid points [m]
(zgr(i),i=1,mzg) (R) z grid points [m]
i j k Bx By Bz (I,R) x-index, y-index, z-index, corresponding field values [T]
The i variable changes most rapidly, then the j variable, then the k variable.
For file format 2 the contents of the user supplied spline coefficient file FOR0##.DAT is
title (a80)
mxg (I) number of x grid points {<101}
myg (I) number of x grid points {<101}
mzg (I) number of x grid points {<501}
href (R) curvature [m-1]
(xgr(i),i=1,mxg) (R) x grid points
(ygr(i),i=1,myg) (R) y grid points
(zgr(i),i=1,mzg) (R) z grid points
nbf(3) (I) # of spline basis functions
nord(3) (I) spline orders
sknot (R) array containing knot sequences
cbx (R) array of spline coefficients for Bx
cby (R) array of spline coefficients for By
cbs (R) array of spline coefficients for Bs
1 model level
1: simple rotating dipole
2: he
3: he
4: planar wiggler
5: he
For model = 1
2 dipole strength [T]
3 solenoid strength [T]
4 wiggler period [m]
For model = 2
2 length of central region, CLEN[m]
3 length for edge region for ramp, ELEN [m]
4 wiggler period [m].This cannot be 0, >0 => right hand twist, <0 => left hand twist.
5 ramp in solenoid field [T]
6 constant solenoid field [T]
7 field ramp for helical dipole [T]
8 uniform field for helical dipole[T]
9 phase offset for helical dipole, phi0 [deg]
10 field ramp for helical quadrupole [T/m]
11 uniform field for helical quadrupole [T/m]
12 phase offset for helical quadrupole, phi0 [deg]
13 field ramp for helical sextupole [T/m^2]
14 uniform field for helical sextupole [T/m^2]
15 phase offset for helical sextupole, phi0 [deg]
For model = 3
2 length of central region, CLEN[m]
3 length for edge region for ramp, ELEN [m]
4 wiggler period [m].This cannot be 0, >0 => right hand twist, <0 => left hand twist.
5 length scale for field ramp, LAMB [m]
6 ramp in solenoid field [T]
7 constant solenoid field [T]
8 ramp in wiggler field [T]
9 constant wiggler field [T]
10 phase offset, PHI0 [deg]
RAMP is given by the average of two TANH functions, one going from -1 to 1 with zero at z=ELEN, the other going from 1 to -1 with zero at z=ELEN+CLEN, both having scale length
LAMB. When the phase shift PHI0=0 => the field component is in the y direction at z=0.
(WIG continued)
For model = 4
2 wiggler period, λ [m] λ > 0
3 vertical wavevector, ky [m^-1]
ky > 0
4 (not used)
5 solenoid field strength [T]
6 number of terms in series {1-3}
7 field strength for n=1, C1 [T]
8 field strength for n=2, C2 [T]
9 field strength for n=3, C3 [T]
10 initial azimuth [radians]
The field components are hyperbo
kx is sinusoidal if ky > 2π / λ
kx
is hyperbo
kx is 0 if ky = 2π / λ
For model = 5
2 wiggler period [m]
3 dipole strength [T]
4 additional solenoid strength [T]
4.2 Material tags and parameters
MTAG (A) material composition tag
Enter MTAG in upper case.
VAC vacuum (i.e., no material)
GH gaseous hydrogen
GHE gaseous helium
LH liquid hydrogen
LHE liquid helium
LI BE B C AL TI FE CU W HG PB (elements)
LIH lithium hydride
CH2 polyethylene
MGEOM (A) material geometry tag
GPARM (R) 10 parameters that describe the geometry of the material.
These 10 parameters must be on one input line.
Enter MGEOM in upper case. Set unused parameters to 0.
NONE use for vacuum
10*0.
CBLOCK cylindrical block
10*0.
n.b. the program tracks thru any of the following types of wedge region with fixed step sizes,
regardless of the value of the parameter VARSTEP.
4.3 Geometry tags and parameters
ASPW Azimuthally Symmetric Polynomial
Wedge absorber region
Edge shape given by
r(dz) = a0 + a1*dz + a2*dz^2 + a3*dz^3 in the 1st quadrant and
where dz is measured from the wedge center.
1 z position of wedge center in region [m]
2 z offset from wedge center to edge of absorber [m]
3 a0 [m]
4 a1
5 a2 [m^(-1)]
6 a3 [m^(-2)]
ASRW Axi-Symmetric Radial Wedge absorber region
Edge shape given by
dz(r) = a0 + a1*r + a2*r^2 + a3*r^3
This is the half-thickness of the wedge. The wedge is symmetric about the x-y plane located at z=ZV.
The wedge material is filled in from z=ZV-dz to z=ZV+dz at any given radius.
1 distance of symmetry x-y plane from beginning of region, ZV [m]
This is typically half the thickness of the s-region. If =0=> left half of wedge is cut off.
2 maximum half-thickness of wedge along z [m] Needs to be > 0.
3 a0 [m]
4 a1
5 a2 [m^(-1)]
6 a3 [m^(-2)]
HWIN hemispherical absorber end region
1 end flag {-1: entrance, +1: exit}
2 inner radius of window[m]
3 window thickness [m]
4 axial offset of center of spherical window from start of end region [m]
The user must specify three “radial” subregions. The geometry parameters (above) and the
maximum cylindrical radial cut off are taken from the first radial region definition. The material
specified in the first radial subregion is the absorber, the material in the second is the window,
and the material for the third corresponds to the outside of the window, e.g. vacuum.
Example
SREGION ! hemishperical
end region (exit)
0.100 5 30.001
1 0.0.173
NONE
0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
LH !LH
HWIN
1. 0.20 500e-6 0.10 0. 0. 0. 0. 0. 0.
2 0. 0.173
NONE
0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
AL
HWIN
0. 0. 0. 0.0. 0. 0. 0. 0.
0.
3 0. 0.173
NONE
0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
VAC
HWIN
0. 0. 0. 0.0. 0. 0. 0. 0. 0.
1 zV distance of wedge “center” from start of region [m]
2 z0 distance from center to left edge [m]
3 z1 distance from center to right edge [m]
4 θ0 polar angle from vertex of left edge [deg]
5 φ0 azimuthal angle of left face [deg]
6 θ1 polar angle from vertex of right edge [deg]
7 φ1 azimuthal angle of right face [deg]
For description see S. Berg, MC note 261, October 2002.
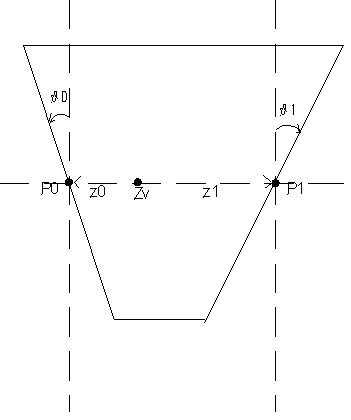
PWEDGE Asymmetric polynomial wedge absorber region
Imagine the wedge lying with its narrow end along the x axis. The wedge is symmetric about the
x-y plane. The edge shape is given by
dz(x) = a0 + a1*x + a2*x^2 + a3*x^3
where dz is measured from the x axis.
1 (not used)
2 initial position of the vertex along the x axis [m]
3 z position of wedge vertex [m]
4 azimuthal angle of vector pointing to vertex in plane of wedge w.r.t. +ve x-axis [deg]
5 total width of wedge in dispersion direction [m]
6 total height of wedge in non-dispersion direction [m]
7 a0
8 a1
9 a2
10 a3
Assume the wedge is initially positioned with the vertex along the x axis (parameter 2). The
wedge is then rotated azimuthally (parameter 4) in the x-y plane to its final position.
1 inner radius (R) [m]
2 outer radius (R) [m]
This is functionally equivalent to defining a region with two radial subregions, the first of which
has vacuum as the material type. However, the boundary crossing algorithm used for RING is
more sophisticated and should give more accurate simulations.
WEDGE Asymmetric wedge absorber region
1 full angle at vertex, α (or A) [degrees]
2 initial position of the vertex along the x axis, U [m]
3 z position of wedge vertex, Zv [m]
4 azimuthal angle φ of vector pointing to vertex in plane of wedge w.r.t. +ve x-axis [deg]
5 total width of wedge in dispersion direction, w [m]
6 total height of wedge in non-dispersion direction, h [m]
“We begin with an isosceles triangle, sitting on its base, vertex at the top. The base-to-vertex
distance is W. The full opening angle at the vertex is A. Using two of these triangles as sides, we
construct a prism-shaped wedge. The distance from one triangular side to the other is H. The
shape and size of the wedge are now established. We define the vertex line of the wedge to
be the line connecting the vertices of its two triangular sides.
Next, we place the wedge in the right-handed ICOOL coordinate system. The beam travels in the
+Z direction. Looking downstream along the beamline (+Z into the page), +X is horizontal and to the left, and +Y is up.
Assume the initial position of the wedge is as follows: The vertex line of the wedge is vertical
and lies along the Y axis, extending from Y = -H/2 to Y = +H/2. The wedge extends to the right
in the direction of -X, such that it is symmetric about the XY plane. (Note that it is also
symmetric about the XZ plane.) From the beam's point of view, particles passing on the +X
side of the Y axis will not encounter the wedge, while particles passing on the -X side of the Y
axis see a rectangle of height H and width W, centered in the Y direction, with Z thickness
proportional to -X.
By setting parameter U to a non-zero value, the user may specify that the wedge is to be
translated in the X direction. If U>0, the wedge is moved (without rotation) in the +X direction.
For example, if U = W/2, then the wedge is centered in the X direction; its vertex is at X = W/2
and its base is at X = -W/2. Note that the wedge is still symmetric about both the XY plane and
the XZ plane.
Next, the wedge may be rotated about the Z axis by angle PHI. Looking downstream in the beam
direction, positive rotations are clockwise and negative rotations are counter-clockwise. For
example, setting PHI to 90 degrees rotates the wedge about the Z axis so that its vertex line is
parallel to the X axis and on top, while its base is parallel to the XZ plane and at the bottom. In
general this rotation breaks the symmetry about the XZ plane, but the symmetry about the XY
plane is maintained.
Finally, the wedge is translated in the Z direction by a distance Zv, so that its XY symmetry plane lies a distance Zv downstream of the start of the region. Usually Zv should be at least large
enough so that the entire volume of the wedge lies within its region, i.e. Zv .ge. W tan (A/2), the
maximum Z half-thickness of the wedge. As well, the region usually should be long enough to
contain the entire volume of the wedge, i.e. RegionLength .ge. Zv + W tan (A/2). Wedges that do
lie completely within their region retain their symmetry about the XY plane Z=Zv.
If portions of a wedge lie outside their region in Z, then the volume of the wedge lying outside
the region is ignored when propagating particles through the wedge. Such a wedge will grow in
thickness until it reaches the region boundary, but will not extend beyond it. In such cases,
wedges may lose their symmetry about the XY plane Z=Zv.
Wedges may be defined such that they extend outside the radial boundaries of the radial
subregion within which they are defined. However, any portion of the wedge volume lying inside the inner radial boundary or outside the outer radial boundary is ignored when propagating particles through the wedge. For example, if the user intends that an entire radial subregion of circular cross-section be filled with a wedge, then it is clear that the corners of the wedge must extend outside the radial region, but particles passing outside the wedge's radial subregion will not see the wedge at all.
In short, we may say that although it is permitted (and sometimes essential) to define a wedge to
be larger than its subregion, for the purposes of particle propagation the wedge is always trimmed at the region's Z boundaries and the subregion's radial boundaries. Any volume within the region and subregion that is not occupied by the material specified for the wedge is assumed to be vacuum.
---------------------------------------------------------------------------------------------------------------
Example 1: Within a region 0.4 meters long in Z, within a radial subregion extending from the Z axis out to a radius of 0.3 meters, a wedge is to fill the X<0 (right) half of the 0.3 meter aperture of the subregion, and increase in Z thickness proportional to -X, such that it is 0.2 meters thick at the rightmost point in the subregion (X=-0.3, Y=0).
The wedge is to be 0.2 meters thick at a point 0.3 meters from its vertex. The half-thickness is
0.1 meters, the half-opening angle is atan (0.1/0.3) = 18.4 degrees, so the full opening angle of
the wedge A is 36.8 degrees. The width (X extent) of the wedge must be 0.3 meters, and the
height (Y extent) of the wedge must be 0.6 meters. Two corners of the wedge extend well beyond the subregion, but they will be ignored during particle propagation. The wedge does not need to be translated in X (U = 0) nor does it need to be rotated about the Z axis (PHI = 0). For
convenience we center the wedge (in Z) within its region, so Zv = 0.2 meters. Since the
maximum half-thickness of the wedge is only 0.1 meters, the wedge does not extend beyond (or
even up to) the Z boundaries of the region. The volume within the region and subregion but
outside the wedge is assumed to be vacuum.
------------------------------------------------------------------------------------------------------------
Example 2: In the same region and subregion, we need a wedge with the same opening angle,
but filling the entire aperture of the subregion, thickness gradient in the +Y direction, thickness =
0 at the lowest point in the subregion (X=0, Y=-0.3).
The wedge must now have H = W = 0.6 meters so it can fill the entire aperture of the subregion.
From its initial position, it must first be translated 0.3 meters in the +X direction (U = 0.3) to
center it in the subregion's aperture, and then (from the perspective of someone looking
downstream along the beam) rotated counterclockwise 90 degrees (PHI = -90.) so that the Z
thickness increases proportionally to +Y. Since the wedge has the same opening angle as before
but has twice the width, its maximum Z thickness is now 0.4 meters, just barely fitting between
the Z boundaries of the region if Zv = 0.2 meters. All four corners of the wedge now extend
outside the radial subregion's outer boundary, but they will be ignored during particle
propagation.” {S.B.}
5. Other files
5.1 Input files
5.1.1 FOR003.DAT Beam input data
This optional file can be used to start a simulation using previously defined beam data.
Title card (A79)
Reference particle data: ZBREF,PBREF,TBREF,ZB2REF, PB2REF, TB2REF,TYPREF. (R)
{ZB, PB, TB} refer to the z position [m], momentum [GeV/c] and time [s] for the reference particle (and for a second reference particle if present). TYPREF is the particle code for the type of particle (cf. sec. 2.4).
For a new problem set this card to seven 0. fields.
This is followed by an indefinite number of incident particles, each with the following data.
(1) IEVT (I) event #(increase sequentially from 1)
(2) IPNUM (I) particle # for this event (set to 1)
(3) IPTYP (I) particle type code (see BMTYPE in sec. 2.4)
(4) IPFLG (I) particle status flag (set to 0)
(5) TP (R) time [s]
(6) EVTWT (R) event weight (set to 1.)
(7) XP(i),i=1,3 (R) cartesian position [m] (set xp(3)=0.)
(8) PP(i),i=1,3 (R) cartesian momentum [GeV/c]
(9) POL(i),i=1,3 (R) cartesian spin vector
For muons from pion decay this vector should correspond to the muon rest frame if spin tracking
is to be done.
5.1.2 Optional files can be used to define the magnetic field on an r-z grid. See BLOCK, COIL,
SHEET and SOLENOID (USER) for descriptions of the file formats.
5.1.3 Optional file can be used to set the parameters of RF cavities using the control variable RFPHASE.
The following is repeated for every RF cavity region.
(1) ID (I) ICOOL region number of the rf cavity
(2) PHASERF (R) cavity phase[degrees]
(3) FRF (R) cavity frequency [MHz]
(4) GRADRF (R) cavity peak electric field on-axis [MV/m]
5.2 Output files
5.2.1 FOR002.DAT program LOG file
This file is always created. It can consist of:
1. print out of input variables used
2. summary table of region properties
3. diagnostic print out of particle position, momentum, spin, and fields (optional)
4. identification of tracks that fail to reach end of the simulation
5. transverse and longitudinal emittances at specified planes (optional)
6. histogram statistics (optional)
7. scatterplot statistics (optional)
8. covariance of particle distributions at specified planes (optional)
9. character histogram of desired quantities (optional)
10. character scatterplot of desired quantities (optional)
11. Z-history (trace) of desired quantities (optional)
12. elapsed time for simulation
5.2.2 FOR004.DAT Beam information after a specified region
This optional file contains particle information in the same format as described for file
FOR003.DAT above.
5.2.3 FOR009.DAT postprocessor data file
This file contains information about each of the particles at production and at various z locations
under the user’s control. This file is generated using the OUTPUT pseudocommand
or the control variables OUTPUT1, NTUPLE and RTUPLE.
Title card (A79)
Header line with units
Header line with column labels
This is followed by particle information at requested positions.
1) IEVT (I) event #
2) IPNUM (I) particle # for this event
3) IPTYP (I) particle type code (see BMTYPE in sec. 2.2)
4) IPFLG (I) particle status flag
5) JSRG (I) ICOOL region #
6) TP (R) time [s]
7) XP(i),i=1,3 (R) position [m]
8) PP(i),i=1,3 (R) cartesian momentum [GeV/c]
9) BFLD(i),i=1,3 (R) total magnetic field [T]
10) EVTWT (R) event weight
11) EFLD(i),i=1,3 (R) total electric field [V/m]
12) SARC (R) total arclength [m]
13) POL(i),i=1,3 (R) spin
For muons from pion decay POL(3) contains the helicity in the LAB frame when SPIN=true and SPINTRK=0.
5.2.4 An optional file can be created of the cy
The contents of the field map is
title (A80)
# of z grid points (I) {1-5000}
# of r grid points (I) {1-100}
i, j, zi, rj, BZi,j, BRi,j (I, R)
Note that the z locations in this file are specified relative to the position where the current field
definition was made, i.e. they are not absolute z locations.
5.2.5 An optional 3D magnetic field grid file can be created using the BACKGROUND command. The format of the file is
title (A80)
nx, ny, nz, hcurv (I, R) # of x, y, z grid points; curvature [m]
xgri, i=1,nx (R)
ygrj, j=1,ny (R)
zgrk, k=1,nz (R)
i, j, k, BXi,j,k, BYi,j,k, BZi,j,k (I, R)
Note that the z locations in this file are specified relative to the position where the current field
definition was made, i.e. they are not absolute z locations.
5.2.6 An optional file can be produced of RF diagnostics at the end of every acceleration region.
(See the control variable RFDIAG.)
(1) JSRG (I) region number
(2) id (I) event number
(3) d(phase) (R) difference (particle-reference) phase at cavity center
(4) dt (R) difference (particle-reference) time at cavity center
(5) dPz (R) difference (particle-reference) Pz at cavity center
(6) f (R) rf frequency [Hz]
(7) G (R) gradient [V/m]
(8) PHASERF (R) cavity phase [degrees]
(9) EZRF (R) cavity Ez [V/m]
(10) BPHIRF (R) cavity Bphi [T]
(11) TREFMEAN (R) zero crossing time of reference particle at center of preceding
cavity [s]
(12) T2REFMEAN (R) zero crossing time of 2 nd reference particle at center of preceding
cavity [s]
(13) Z (R) Z for particle at center of cavity [m]
5.2.7 Neutrino production data
This data appears on the file specified by the control variable NEUTRINO.
Title record (A)
Problem title (A80)
For each neutrino satisfying the polar angle cuts:
1) IEVT (I) event #
2) IPNUM (I) particle # for this event
3) IPTYP (I) particle type code
4) IPFLG (I) particle status flag
5) JSRG (I) ICOOL region #
6) TP (R) time [s]
7) XP(i),i=1,3 (R) position [m]
8) PP(i),i=1,3 (R) cartesian momentum [GeV/c]
9) EVTWT (R) event weight
The particle type uses the following code
6 muon neutrino
-6 muon antineutrino
7 electron neutrino
-7 electron antineutrino
±20 from muon decay
±30 from pion decay
±40 from kaon decay
e.g. IPTYP = -36 for a muon antineutrino from pion decay
Problem title (A80)
At each OUTPUT command
1) region number
2) Bz [T]
3) t [s]
4) Pz [GeV/c]
5) normalized transverse emittance [m rad]
6) Courant-Snyder beta [m]
7) Courant-Snyder alpha
8) angular momentum
9) particle number
10) transverse scraping parameter
11) normalized longitudinal emittance [m rad]
A summary of all regions (and pseudoregions) in the job is
written to the for007.dat if the control variable SUMMARY is true.
(1) FOR008.DAT particle overflow data file
This unformatted, direct access file contains particle data used by the program. It is only created
when the number of requested particles is greater than 300,000.
6. Program execution flags
0 No errors.
-1 Fatal error (with message on the log file)
-10 particle outside dipole aperture
-11 got unphysical momentum from dipole edge focusing
-12 negative argument for SQRT {DERIV]
-13 error setting angular momentum correlation
-14 got unphysical momentum computing random field kick
-15 event failed because of variable cut
-16 error creating initial dispersion
-23 Particle radius not in defined r-region.
-24 failure of Fano scattering model
-25 Illegal LOG argument [DEDX]
-26 failure of Tollestrup scattering model
-27 Illegal LOG argument [SCATTER]
-28 Particle outside an aperture [SIMULATE]
-29 probability error [RESTRICT_LOSS]
-30 error in muon decay
-31 exceeded allowed radius in the tapered solenoid
-32 Vz went negative [GO_REGION]
-33 stuck in stepping loop[GO_REGION]
-36 particle time difference exceeded BUNCHCUT [SIMULATE]
-39 r > r(cav) [ACCEL ]
-40 r > r(rod) [TAPERED_ROD]
-43 Pz of particle is less than control variable PZMINTRK
-47 particle transverse position outside the kicker cavity
-52 particle decayed
-57 radius > Rcav in Superfish model
-58 failed absorber hemispherical end region logic
-61 momentum outside desired band for induction linac
-62 spin tracking error [GO_REGION]
-64 depolarization error [FLIP_ELASTIC]
-72 radius too large in HELIX
-73 hadron had inelastic interaction (tracking stops)
-74 argument out of range in Bessel function I0 or I1
-75 argument out of range in Bessel function K0 or K1
-76 stepping gave result with r > 100 m or pt > 1000 GeV/c
-77 error in ACCEL model 10; two ref particles have same p?
-81 interpolated HORN point lies outside data grid
-82 position error in DIPOLE model 4
-85 failure of MOLIERE scattering algorithm
-86 got unphysical momentum computing hard-edge fringe field kick
-87 unphysical momentum from TRANSPORT matrix