NFMCC NFMCC

International Scoping Study
Machine Working Group
US FFAG Specifications

The lattice is a doublet lattice with a short drift and a long drift, the latter potentially containing an RF cavity. The RF cavities have a maximum gradient of 17 MV/m. The two magnets are labeled "D" and "F," reflecting the sign of their gradient. Note that in addition to the baseline 5–10 GeV and 10–20 GeV FFAGs, there is also a 2.5–5 GeV FFAG. The 2.5–5 GeV FFAG was of comparable cost per GeV to the Study II RLA, and was thus considered to be too costly for the updated design. However, when compared with the cost per GeV of the RLA that goes up to that energy, it may be more cost effect to use the FFAG. Thus, the 2.5–5 GeV FFAG is included here for the purposes of deciding whether to add that stage. Yes, the precision is excessive. This is based on an optimization process by J. Scott Berg.

Minimum Total Energy (GeV) 2.5510
Maximum Total Energy (GeV) 51020
Cells 526484
Short drift (m) 0.50.50.5
Long drift (m) 2.02.02.0
D angle (mrad) 156.4442206142160 134.6062650623434 104.6686081591161
D length (m) 0.5958624007498240 0.7472149648887136 0.9253951702451095
D displacement (mm) 30.19651030200021 24.66640953767451 20.72963873834226
D dipole (T) 2.997813333585663 4.191313218599995 5.289153187390601
D gradient (T/m) -12.56336682952998 -19.13765556626068 -29.03074550693176
D aperture radius (mm) 131.8774731795656 98.33278241799703 75.08345310239752
D aperture field (T) 4.654638405692046 6.073172139387677 7.468881806187950
F angle (mrad) -35.61373393768555 -36.43149463766231 -29.86878307364487
F length (m) 0.9514300864320404 1.198233028254445 1.451173111123141
F displacement (mm) -8.931878344742322 -6.227979543072953 -4.970803353204361
F dipole (T) -0.5312320109312531 -0.8003561249393034 -1.061970351096813
F gradient (T/m) 10.35041414019155 15.38155440293255 23.69759841076119
F aperture radius (mm) 207.4326841609991 166.0854534894128 129.9898743301357
F aperture field (T) 2.678246198209145 3.355008563322430 4.142418190437684
RF Cavities 424654
Energy Gain per Cavity (MeV) 12.52984394532481 12.39644070260180 12.64502711350376
Turns 4.803021358170473 9.012597500995915 15.44969574802365
Circumference (m) 210.4908297248826 284.5447937784257 409.6672306170535
Time of flight range, per cell (ps) 18.51244338195651 12.58317050455552 7.720029576745513

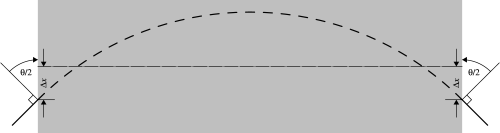
The lattice uses so-called "rectangular bends," where the central axis of the magnet is straight, not curved. The following diagram illustrates the meaning of the angles and displacements for these magnets:

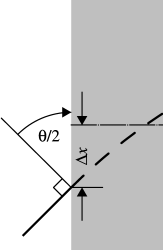
RBend
RBend

First the coordinate system is rotated by an angle θ/2 (θ is the "angle" above) such that for positive θ, a particle initially with zero angle would now have an angle of θ/2 in the positive x direction. Next, the coordinate system is displaced by an amount -Δx (Δx is the "displacement" above), meaning that a particle initially at x=0 now has x=-Δx. Then one tracks through the magnet in a straight coordinate system, with x=0 being the center of the magnet. The field and gradient given above are on the central axis of the magnet. Next, the coordinate system is displaced by Δx. Finally, the coordinate system is rotated by an angle θ/2. The length of the magnet is the length of the (straight) central axis above, not the arc length of some "reference particle."